该笔记主要对inference部分的理论进行回顾和整理

1 introduction

之前主要介绍的是表示部分，也就是如何根据概率图模型的图结构了解变量之间的独立性以及写出联合概率。

通过表示部分，我们可以对于一个具体的多变量影响因素的问题快速的根据各个变量之间的相互作用构建出概率图模型的网络结构

但仅有网络结构是不足的，我们还需要利用网络去做以下的两件事：

• 推断（inference）
• 学习（learning）

其中，推断就是在网络结构和权重已知的情况下，推断出概率分布；而学习则是希望网络在一次次的学习中更新网络权重。

类比神经网络的话，推断做的就是把数据输入到已经训练好的神经网络模型中，做predict；而学习做的就是把数据放入网络中，使得网络可以learning并更新权重

今天主要总结的是inference

2 Variable Elimination（变分消元） introduction

变分消元法是一种前向传播的算法，他通过父节点的信息来进行消元，进而得到子节点的表达式

例如对于以下的一个贝叶斯网络：

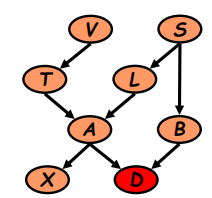
根据表示部分我们可以很快的利用因子分解定理写出联合分布：
\(P(V)P(S)P(T|V)P(L|S)P(B|S)P(A|T, L)P(X|A)P(D|A,B)\)

可以简写一下：
\(\phi_V(V)\phi_S(S)\phi_T(T,V)\phi_L(L,S)\phi_B(B,S)\phi_A(A,T.L)\phi_X(X, A)\phi_D(D, A,B)\)

要获得最末端的子节点D的分布概率$P(D)$，最好的方法就是从上往下消元（从父节点往子节点，最开始的父节点没有父节点，那么其因子分解定理的式子里的概率表达式就他自己，例如P(V)，P(S)等）

由于网络来说，V节点是最上层的父节点，影响的因素最少，所以我们可以从他开始：

对于V节点：
\(\tau_1(T)=\sum_V \phi_V(V)\phi_T(T,V)=P(T)\) 那么上述的联合概率（2）就可以代入（3）得到：
\(\tau_1(T)\phi_S(S)\phi_L(L,S)\phi_B(B,S)\phi_A(A,T.L)\phi_X(X, A)\phi_D(D, A,B)\) 在处理了V之后我们可以同样处理S节点：
\(\tau_2(L,B)=\sum_S \phi_S(S) \phi_L(L,S)\phi_B(B,S)\) 将（5）代入（4）可以得到：
\(\tau_1(T)\tau_2(B,L)\phi_A(A,T.L)\phi_X(X, A)\phi_D(D, A,B)\) 同理可以进一步消除得到：
\(\tau_3(A)=\sum_X \phi_X(X,A)\\ \tau_4(A,L)=\sum_T \tau_1(T)\phi_A(A,T,L)\\ \tau_5(A,B)=\sum_L\tau_4(A,L)\tau_2(B,L)\) 此时经过这么多步的消除之后原先的联合分布式已经消元成：
\(\tau_5(A,B)\tau_3(A)\phi_D(D,A,B)\) 进一步把A的内容消除得到$\tau_6$
\(\tau_6(B,D)=\sum_A \tau_5(A,B)\tau_3(A)\phi_D(D,A,B)\) 此时因子分解式被代入后变为：$\tau_6(B,D)$，应用全概率公式消除B即可得到最末端的D的概率$P(D)$

上述就是最为基本的变分消元的过程

3 induced graph in VE

在给定了部分变量观测值之后，有向图中面临了不少的V-structure：

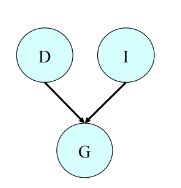
例如上图给定了G的值之后，会导致原先独立的D和I两个变量不再独立，这会增加我们后续处理的难度

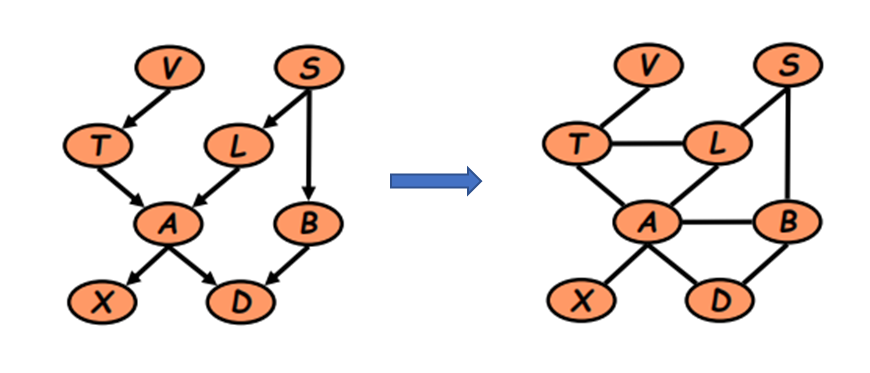
所以想通过induced graph的方法来简化有向图，消除v-structure

做法就是将所有有向图的→的边用无向图的-代替，同时将v-structure的父节点连起来构成三角形，之后还会进行三角化

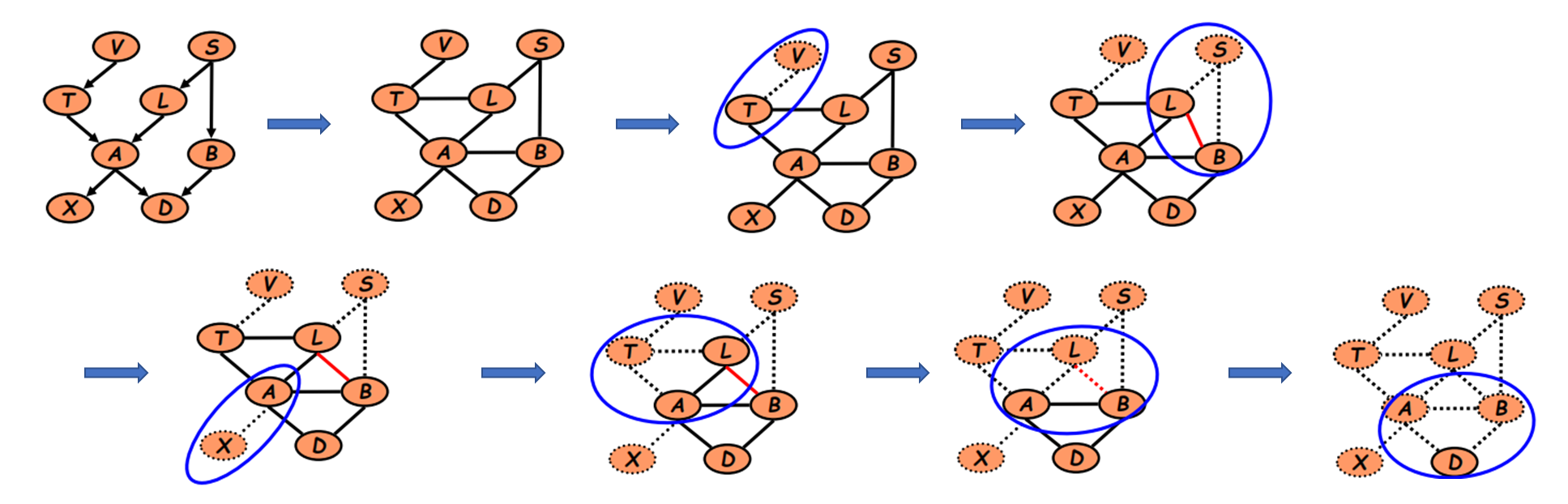
在进行完上述处理后再进行2.1中的变分消元过程：

4 clique tree

4.1 introduction

上述的变分过程面临一个比较重要的问题就是，我们每次推断都需要从上往下整个网络计算一遍，没有利用好中间变量减少计算量，所以我们希望在这方面进行改进

而上述的变分过程从图中看是对每一个clique进行处理（消元/传递信息）

在马尔可夫网络（Markov Network）中，基本单元称为团（cliques）。这是指图中任意两个节点都直接连接的最大完全子图。具体来说：

1. 团的定义：
   • 一个团是一个子图，其中每对节点之间都有边连接。
   • 最大团是图中不能再扩展的完全子图。

因此，概率图模型的研究者将上述的clique处理过程抽象出来，构建了clique tree和passing message来代表上述的VE过程：

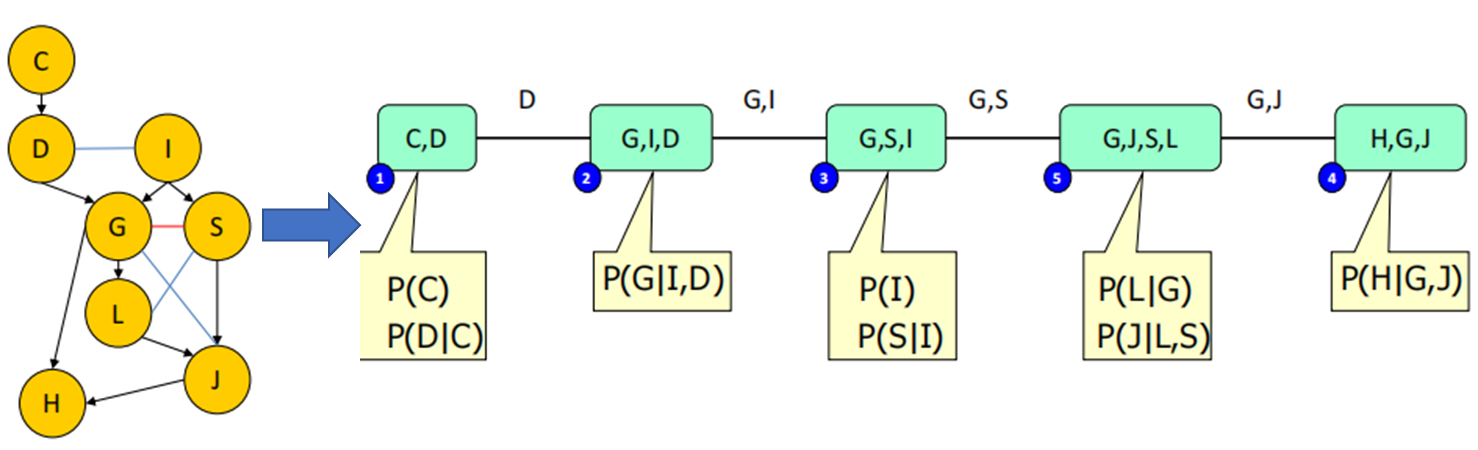
那么以求P(J)为例

上述的有向图被抽象成：

消除C：clique1(C,D)向clique2(D,I,G)传递信息$\delta_{1→2}(D)$

消除D：clique2向clique3传递信息$\delta_{2→3}(G,I)$

需要注意的是：

团树是模型的等价表示
另一种数据结构
；在团树上进行求和乘积消息传递
“等于”变量消除

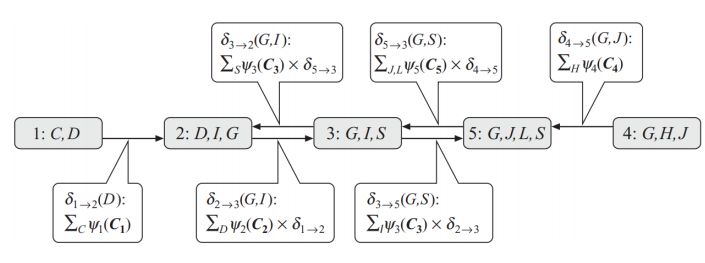
4.2 clique tree校准

仅有clique tree这种相较于概率图的抽象表示并不能解决我们上述提到的VE的困难，为了解决这个问题，利用好VE过程的中间变量来简化计算，我们需要对clique tree 进行校准

所谓校准就是先将上述信息传递都传一遍（VE一遍）使得每个local clique都有全局的信息：

• 对于每一个clique，其都有一个初始的分布函数（或者叫做势函数）：$\psi=\Pi (factors*weight)$
• 然后选择一个根节点，从各个节点向根节点传播信息，也就是上面的$\delta$，此时受到信息的clique其势函数$\psi$会更新：$\psi_{new}=\psi*\Pi(\delta)$ 即原先的势函数乘以其受到的所有信息
• 在整个clique tree经过一轮双向信息传递之后就实现了校准，可以用势函数来表示概率了：

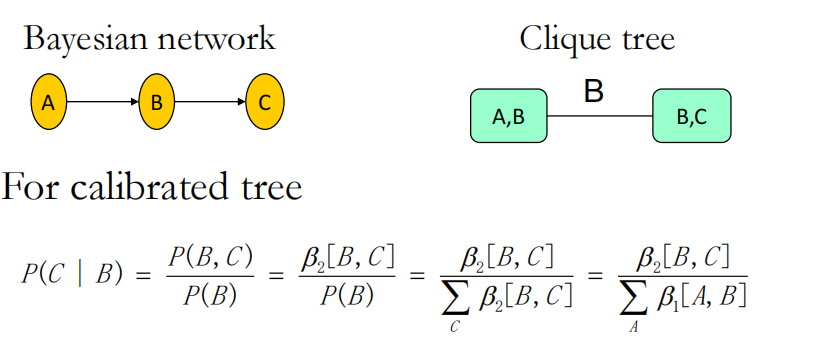
而且由于校准后所有的势函数都已经有了，所以计算任何节点的概率都只需要利用势函数计算即可了

传递信息的过程也被称之为信度更新（belief updating）

5 Variational Inference

变分推断的基本逻辑就是将原有的分布以更为简单的分布去代替，进而获得简化。后续只需要对Q进行推断就可以了而不需要在复杂的P上推断

那么应该怎么才能构造出合适的Q以代替P呢？这里采用了散度+熵的形式

KL散度用以描述Q和P的相似性： \(\min_Q\ D_{KL}(Q||P)\) 而Q的熵则用于描述Q的复杂度，因为如果不加这一项的话，为了使得Q和P接近直接就变成Q=P了，并没有起到简化的作用，只有增加一项Q的复杂度的项才能避免上述情况的发生

那么我没需要的就是找到一个Q使得： \(L(Q)=\max_Q(E_{x \sim Q}(lnP(X,z))+H(Q(X)))\\ =lnP(z)-D_{KL}(Q||P)≤lnP(z)\)

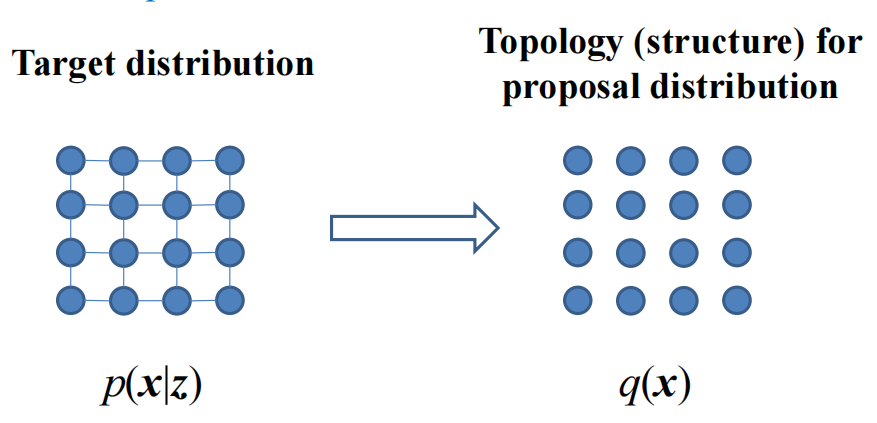
6 Mean field Inference

平均场模型的基本死了就是构造一个没有边的模型作为q去代替原先右边的p分布：

由于q对应的平均场模型是没有边的，所以其分布是很好写的（相当于所有节点都是独立的） \(q(x;\theta)=\prod_i q_i(x_i)\) 代入到上述的$L(Q)$的式子： \(L(q)=\sum_x[\prod_i q_i(x_i)][ln p(x,z)-\sum_k lnq_k(x_k)]\) 这里的L就是优化函数（类似loss一样），我们要的就是不断迭代Q使得其沿着L的方向接近P