该笔记主要介绍了蒙特卡洛近似,包括likelihood weighting和importance sampling
1 Two Strategies for Inference
-
Inference as optimization
- Belief propagation on cluster (or factor) graph
- Structured varational inference
-
Back to the frequentist probability
- Likelihood weighting, importance sampling
- MCMC: Gibbs sampling, Metropolis-Hastings algorithm, Hamiltonian Monte Carlo, Langevin Monte Carlo (sampling Markov blanket posterior)
变分法是极致上限的,上两周的推断主要介绍的1变分推断,还有一部分的是回归频数概率的推断
蒙特卡洛方法的基本逻辑就是从P中产生一堆高效的独立同分布的样本,然后根据频数来近似概率: \(P(X)\approx \frac{n_x}{n_{total}}\) 所以最关键的问题就是如何高效的产生这些样本
2 Forward Sampling
根据网络的结构产生样本,然后最后做统计
需要注意的是,所有参数都是已知的
下图展示的就是根据概率表进行采样的过程
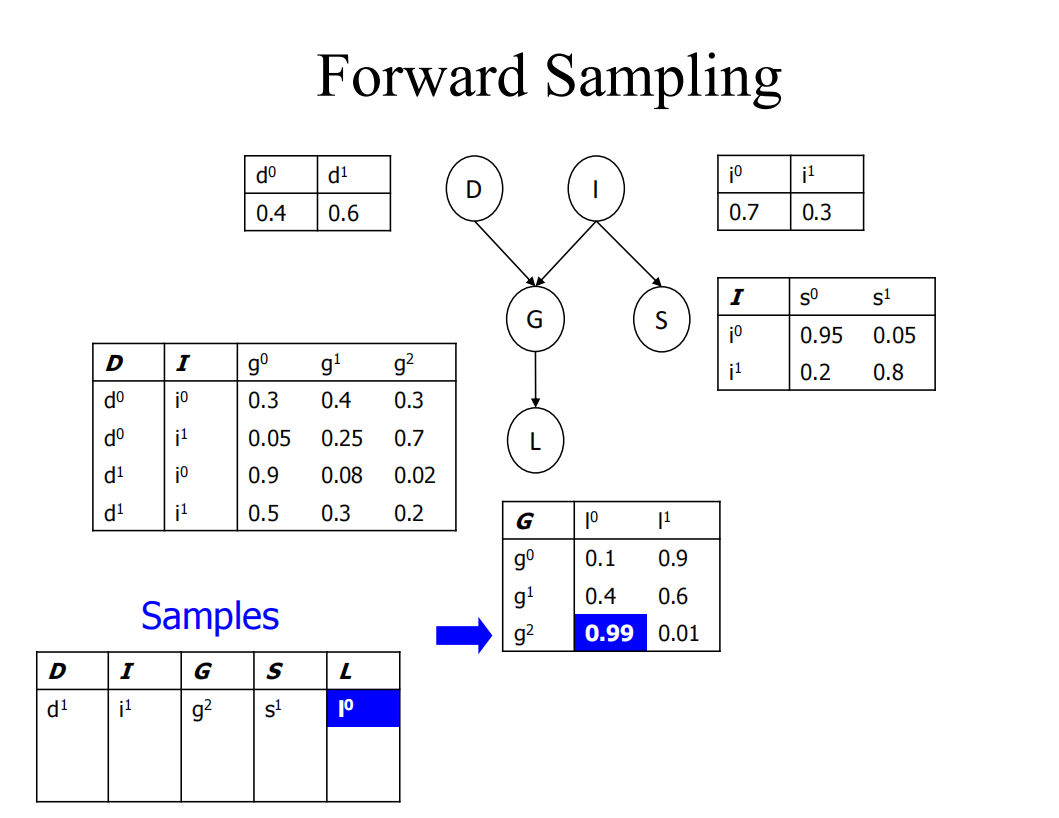
先根据D的概率分布表来随机采样一个d,I也同理,再根据i和d的值以及G的概率分布表得到g,以此类推s和l
| 频数论对于求条件概率也很简单,只需要将分母里的所有样本量,变成满足条件的样本数就行了 P(Y | E=e) |
需要注意的是,采样的数目越多,频数越接近真实概率,那么我们应该选取多少采样数才能尽可能的偏差小呢
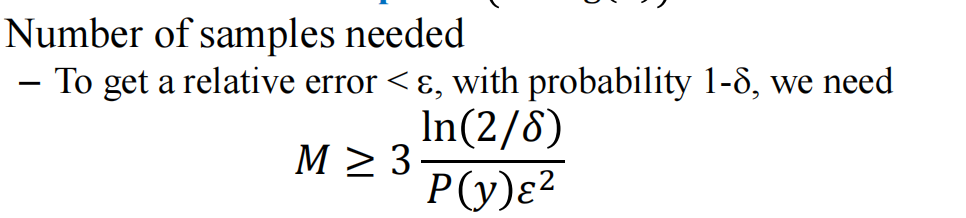
但面临产生一堆样本可能会浪费的情况: \(P(x_3=1,x_5=0|x_2=0)=\frac{N(x_3=1,x_5=0)}{N(x_2=0)}\) N代表频数
3 Likelihood Weighting
| 如何简化呢,上述频数描述的是 P(Y | E=e),我们可以直接设定E的数为e而不进行采样,此时得到的整个结果是 P(Y,E=e),和原先的 P(Y | E=e)相差一个 P(E=e) |
举个例子:
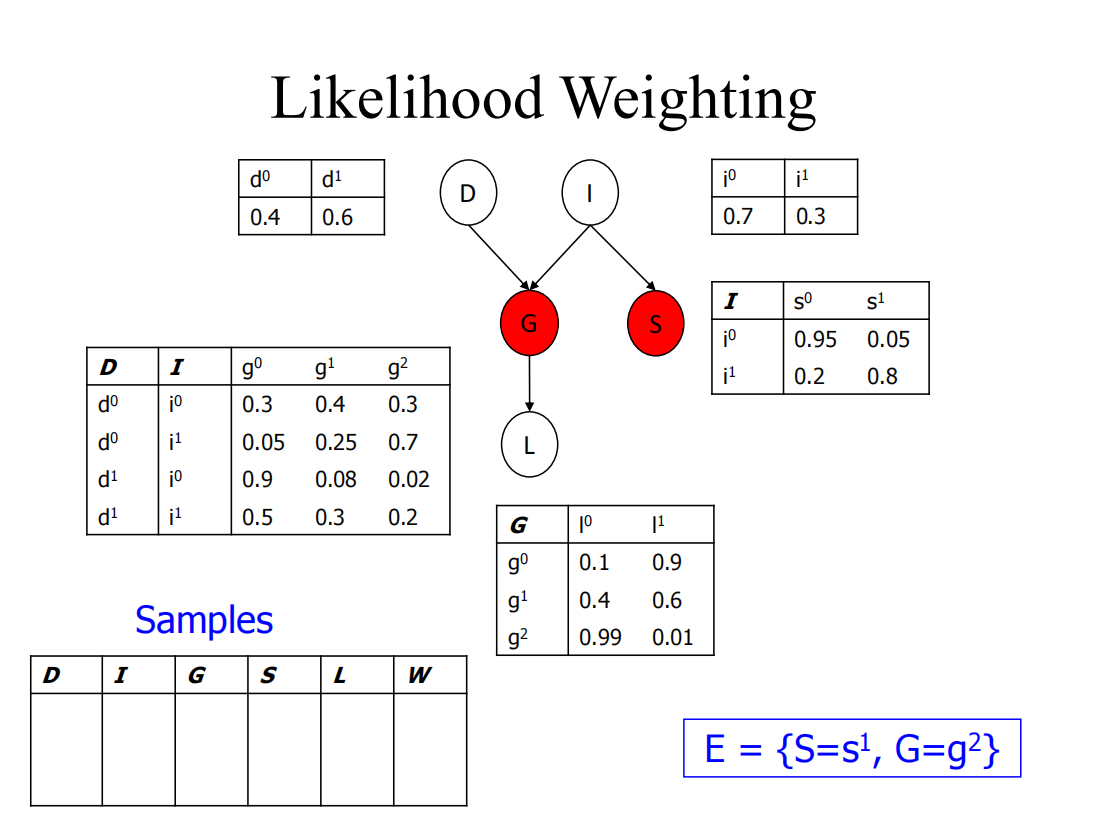
给定G,S的时候,D和I的后验概率其实已经发生改变,不能够按照原先的方法去使用D和I开始生成了
但上述说了的处理方法:
首先G和I还是根据表格随机采样,然后G时强制G等于2(g2),S也是强制等于,记录一个$weight=P(S=s^1)P(G=g^2)$
对于有向图来说likelihood已经可以很好的解决了
4 Importance Sampling
Q的定义域比P大需要,样本在Q中产生而不是P以简化采样,凡是P/Q>1就相当于他的权重增加,小的地方就降权重就行了
公式:
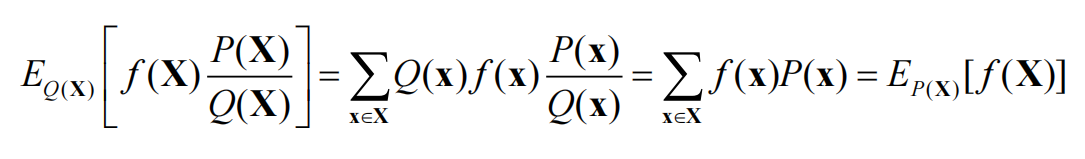
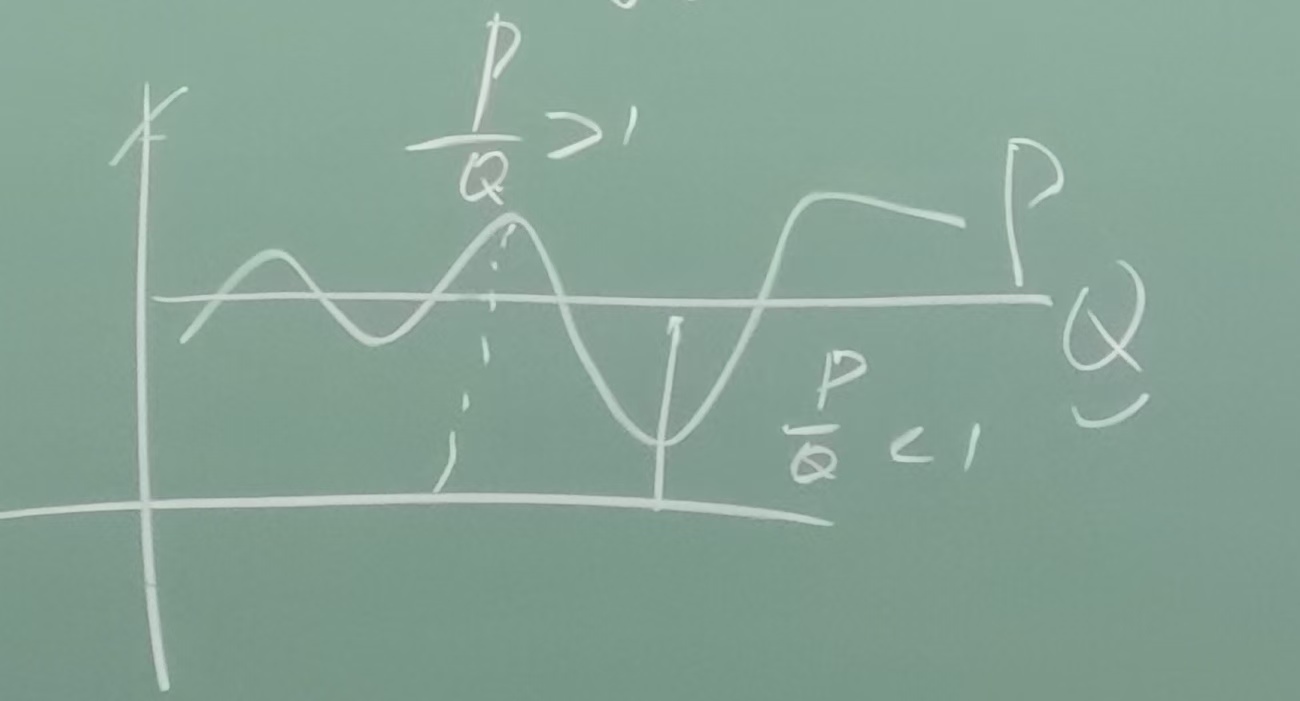
如果P和Q接近的时候,近似开销最少,而如果相差很大则需要额外补充采样
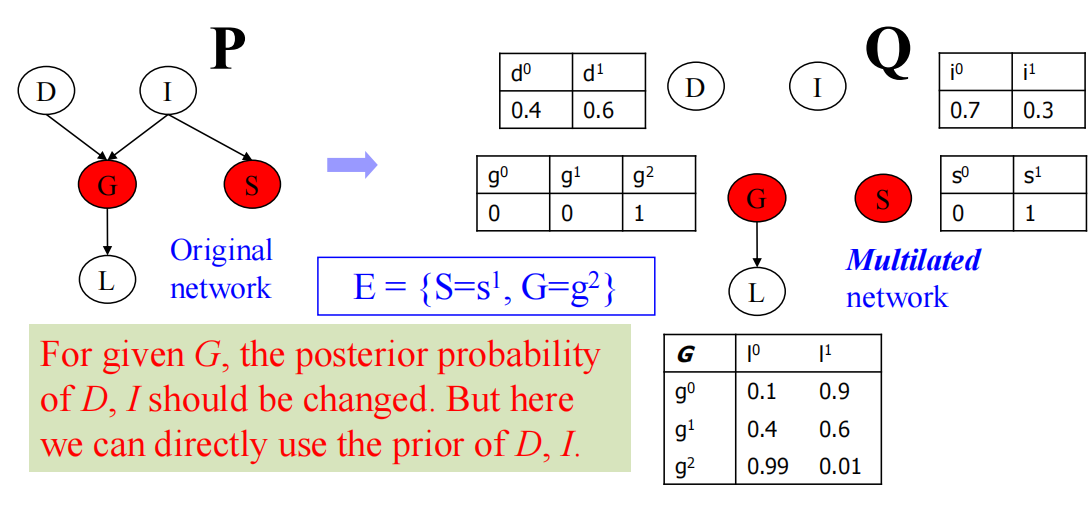
简化操作:凡是有观测的节点,把其和父节点的关联全部删掉,得到multilated network
likelihood weighting是importance sampling的特例(按照上述切割规则设计Q的时候)
关于样本数:
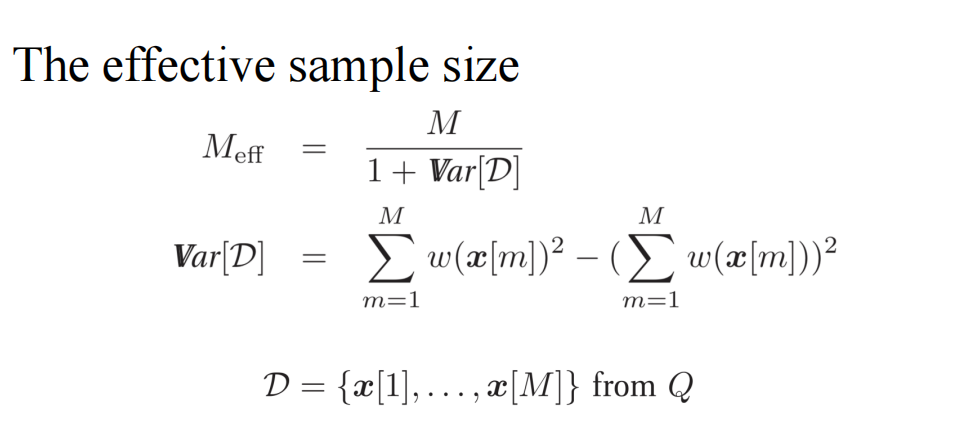
上面这一套对于无向图来说是不太合适的,因为需要将无向图转化成有向图,同时对于无向图不是很好选择Q
5 玻尔兹曼分布与MCMC
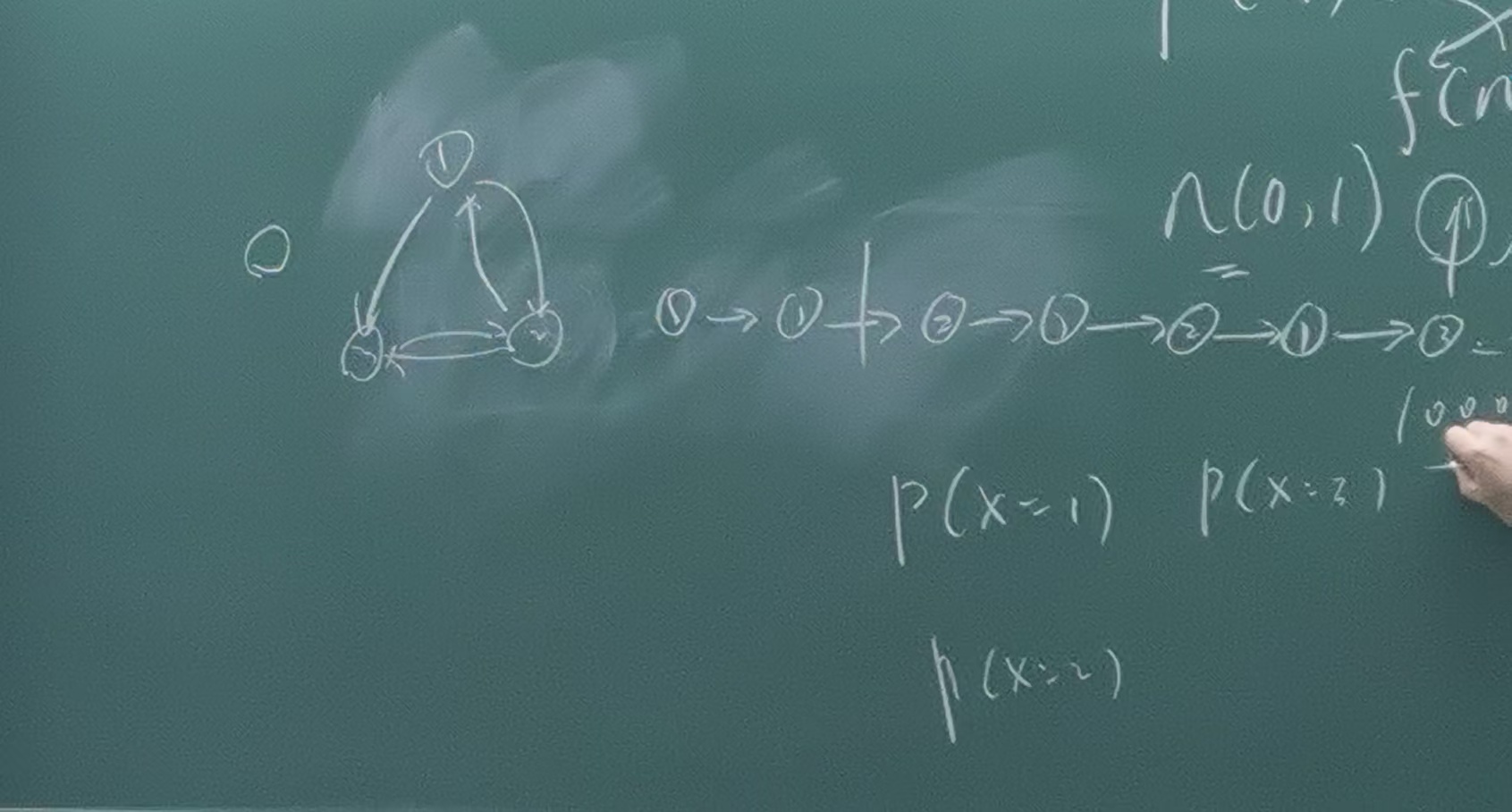
三个粒子状态可以互相转换,当前状态仅与上一时刻的状态有关(马氏性),那么当时间长了之后粒子处于各个状态的概率服从玻尔兹曼分布
能不能设置一个马尔可夫链,使得马氏链的稳态满足目标分布
需要注意importance sampling和likelihood weighting产生样本时与上一个时刻的样本无关,而Markov Chain Monte Carlo则与上一时刻有关
为了避免无穷大/多个稳态分布,所有的local CPD都加上很小的一个数(使得概率为0变成概率变成一个小量)
5.1 最简单的MCMC算法:Gibbs采样
吉布斯采样的转移概率是按照p分布按以下方式设定的: \(𝑇(𝑿(𝑡) = 𝒙 → 𝑿(𝑡+1) = 𝒙′)= 𝑃(𝑿(𝑡+1)|𝑿(𝑡), 𝒆)\) 只有当所有local CPD都是大于零的才能使得所有状态都是常返的

对于常返的条件是:

具体看怎么采样:
5.3 贝叶斯网络的吉布斯采样
首先确定马尔可夫blanket
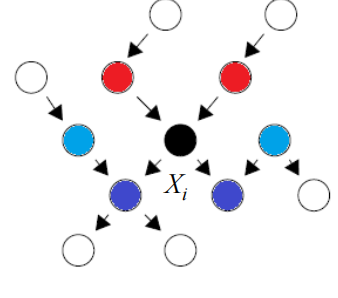
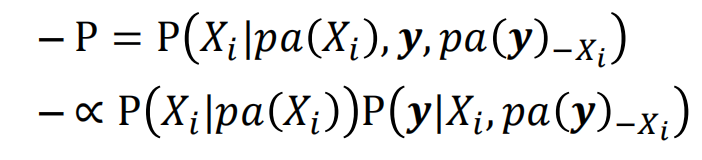
y是x的子节点,上述概率乘积是小于等于1的,不是概率,需要对其进行归一化后才是概率

6 Metropolis-Hastings Algorithm
怎么根据已有的随机生成器Q设计马尔可夫链
设计了配平函数acceptance probability,将P大于Q的部分引入A来配平,Q大于P的部分则不管