该笔记介绍了变分推断以及平均场近似相关的内容
没办法构建clique tree做精确的分布计算，因此提出了变分推断来做近似推断
变分法后面是有完备的理论体系的
1 目标转换（从P到Q)
起因：随着网格结构的增加，P(X)的推断变得越来越困难，因此我们想用一个更加简单的Q(X)来进行拟合，从而可以代表P(X)的话，未来做推断的时候只需要在简化后的Q(X)上进行推断就行，而不需要在比较复杂的P(X)上进行了
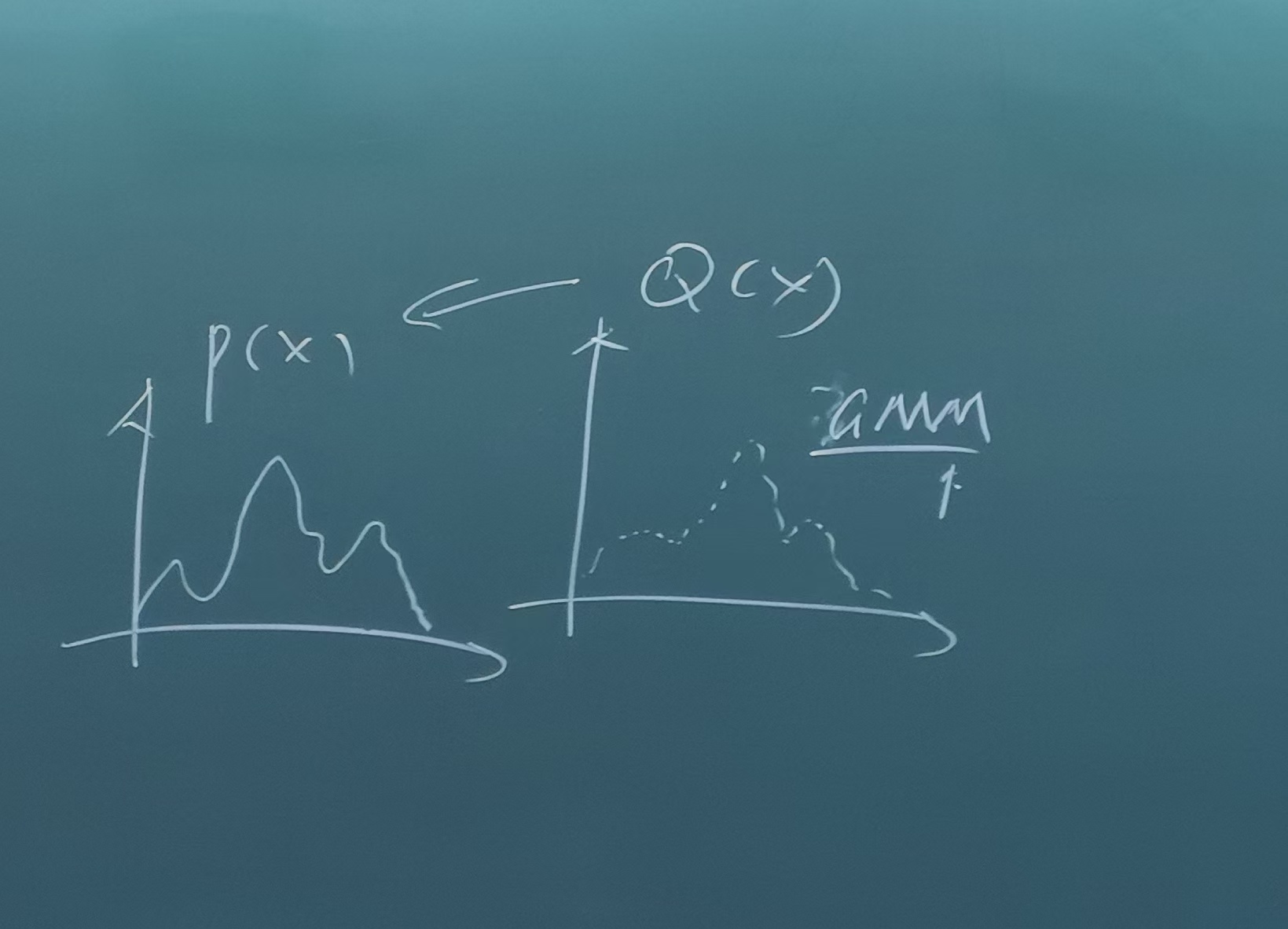
以上就是变分法的基本逻辑
因此我们需要严格定义一个物理量来计算这个P(X)和Q(X)的相似程度，这里用的是KL散度来描述差距：
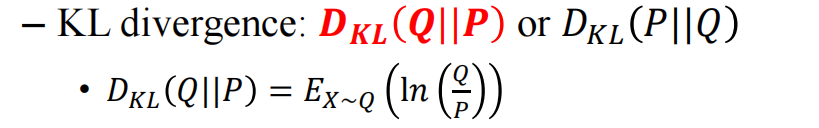需要注意的是，Q和P的前后顺序是不对称的，P在前Q在后和Q在前P在后的散度是不一样的
目标就是在Q的定义域里找一个Q，以达到Q和P的散度最小：
\(\min_Q\ D_{KL}(Q||P)\)
然后我们也是尽可能的定义Q(X)在简单的图结构上
reverse KL就是至少model一个峰
forward Kl则要求至少全都覆盖
在实际操作中我们通常用reverse KL散度：
\(D_{KL}(Q||P)=E_{X\sim Q}(ln \frac{Q(X)}{P(X|z)})\)
这里对Q求期房显然是更加方便的，如果用forward散度就得对P求期望了
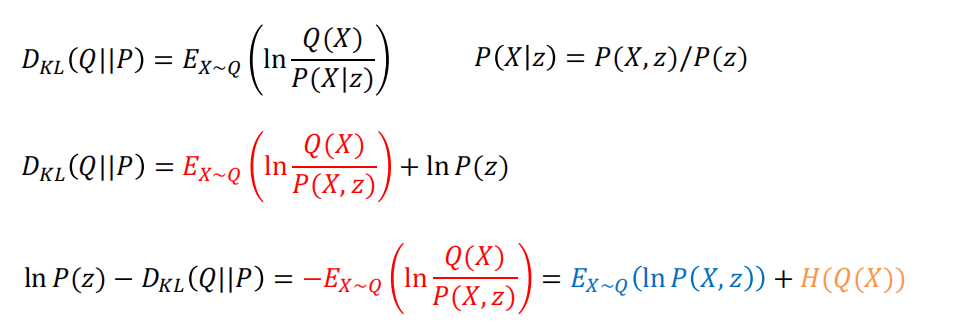其中$E_{Q}(lnQ)$就是Q分布的熵
经过上述等价之后我们的目标变成了
\(\max_Q(E_{x \sim Q}(lnP(X,z))+H(Q(X)))\)
在物理里面叫做能量函数最大化（$\max_Q L(Q)$)或者最小化J(Q)=-L(Q)
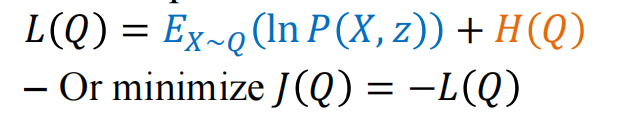
当Q和P像的时候第一项会比较合适，但此时第二项要求Q尽可能平均，这就使得其和第一项的结果背离，通过这两项来实现兼顾两个项
找
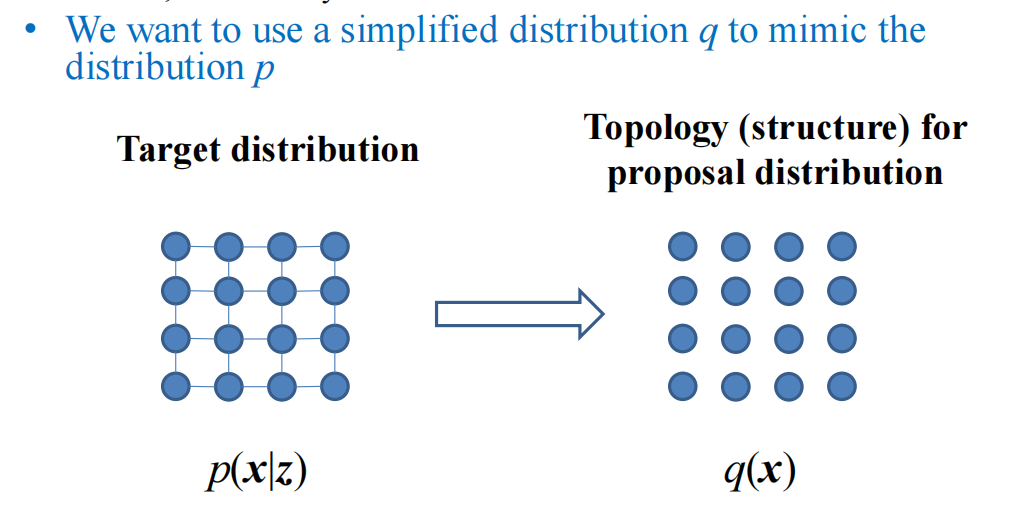Q的时候:
需要限定Q的定义域、需要评价Q和P的相似度，在确定了这些之后就将整个问题变成了找Q实现上述的目标的优化任务了
2 平均场模型
希望构造一个没有边的图模型的Q（也就是所谓的平均场 Mean field inference）
例如：
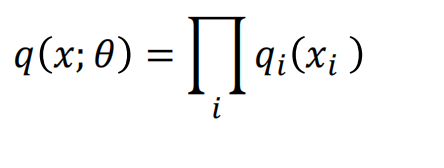现在的Q分布按照概率图模型来说，每一个节点上都有一个自己的边缘分布，而且彼此独立所以连乘起来就是联合分布：
\(q(x;\theta)=\prod_i q_i(x_i)\)
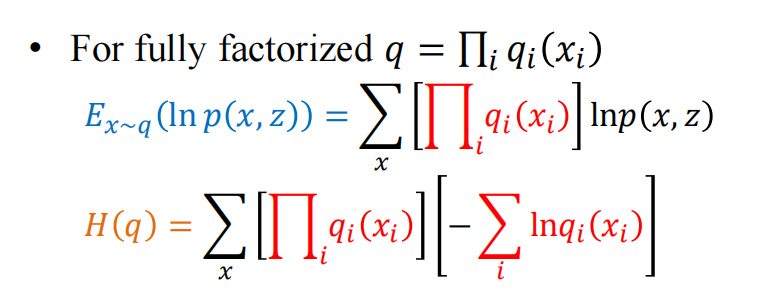
最后合起来两项就是L(q)
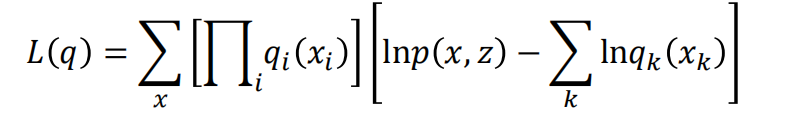优化的时候一次性优化比较难，所以现在我们希望一个q一个q的优化，在优化特定的q的时候，其他的q都固定不动：
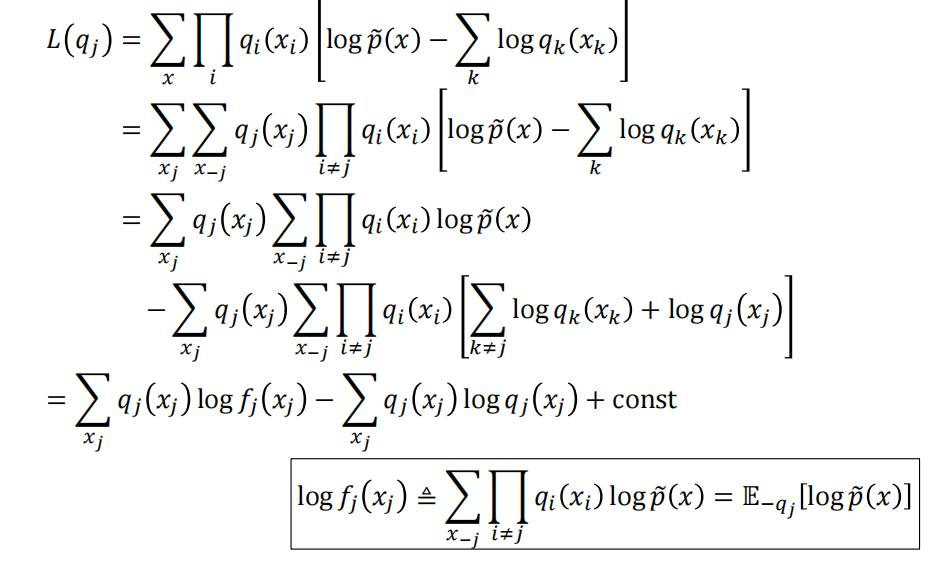最后的结果为：
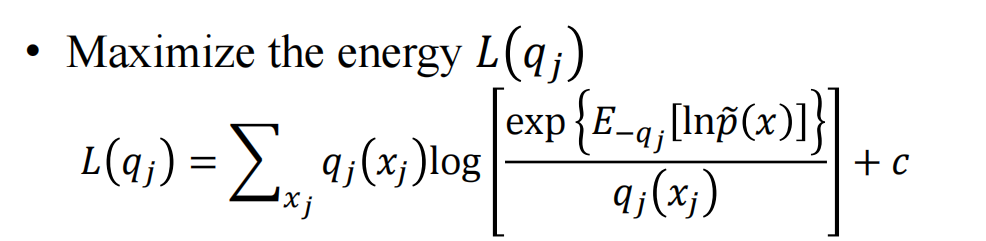当：
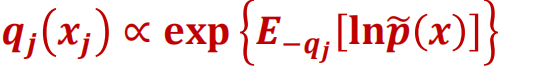此时只需要满足上述就可以使得L(q)达到最大
3 平均场模型实例
现在的目标就是找到最优的Q去模拟下述的问题的P:
ising模型里没有一阶项（惯例）
解决了P~(X)之后再去看q分布的设计
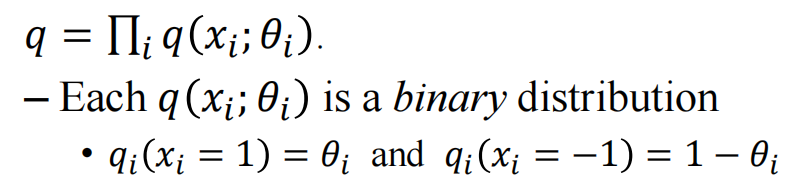继续简化P~(X):
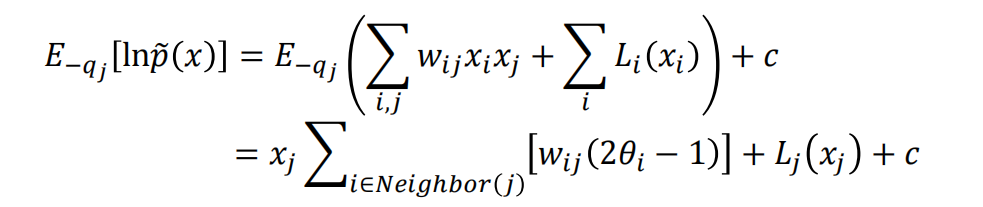对于网格模型，凡是和j节点没有直接相连的边在求期望之后都变成了常数进而都放入c中不影响结果了
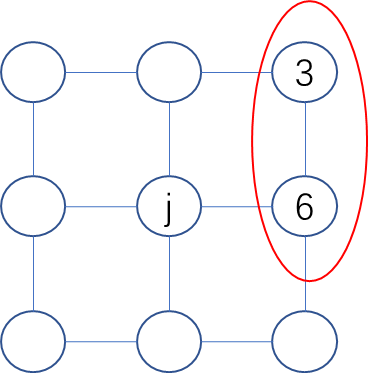例如图中的3-6节点项$w_{3,6}x_3x_6$
而且由于q是二项分布1~θ,-1~(1-θ),所以求期望就是1* θ -1（1-θ)=2θ-1
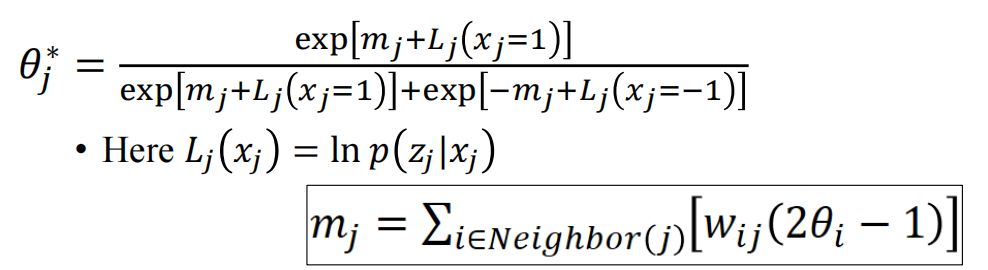**这里的变量是而止变量是取-1和1的，但是如果是0，1分布的那就不能这么用了，例如限制性玻尔兹曼积的话，那么二值是取1和0的，此时就是$w_{ij}\theta_i$ **
对于例题：
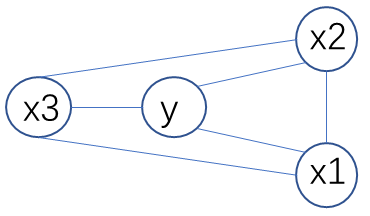\(ln P(x,y)=\frac{1}{z}e^{\alpha_1 x1+\alpha_2 x2+\alpha_3 x3+\beta y+w_{1,2}x_1x_2+w_{1,3}x_1x_3+w_{3,2}x_3x_2+h_1
x_1y+h_2x_2y+h_3x_3y}\)
那么此时
\(\)
E_{q_1(X)}(h_1x_1y)=h_1\theta_1y
$$
\(E_{q_3(X)}(h_3x_3y)=h_3\theta_1y\)
平均场/变分推断做去噪的效果很好：
对于二值问题是可以比较方便的实现求解析解，但有时候并不能直接求解解析解，那么现在可以通过随机梯度来做梯度下降
当变分都完成了之后，只需要全都用q算就行了，不需要再在p中进行求解了，这就是变分的意义（一切后续的计算都用q来计算）
4 NN for variational inference
在数据特别复杂的时候变分函数很难设计：
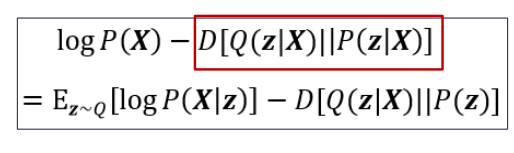这两项就可以用神经网络的encode和decode实现
实际上做的是变分推断
VAE就相当于是对Variation学比较复杂的q通过神经网络