该笔记主要介绍了推断部分的graph cluster相关理论，以及使用clique tree进行准确推断

全新的章节：整个机器学习的核心就是inference
inference：模型的所有参数都是已知的，需要根据模型做概率推断
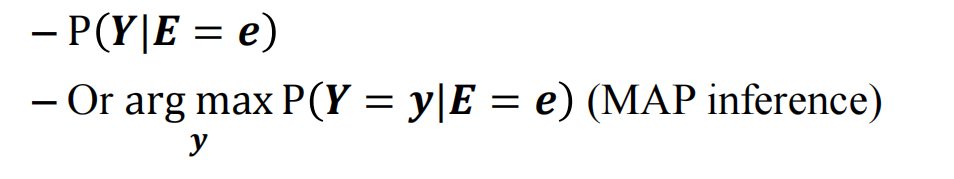任务1：求整个y的概率分布
任务2：求点估计（也就是条件概率y的极大值点)
显然任务1获得的信息量更多，但是也意味着任务1更难以实现
**inference的核心就是求后验概率 **

1 简单的贝叶斯链式网络

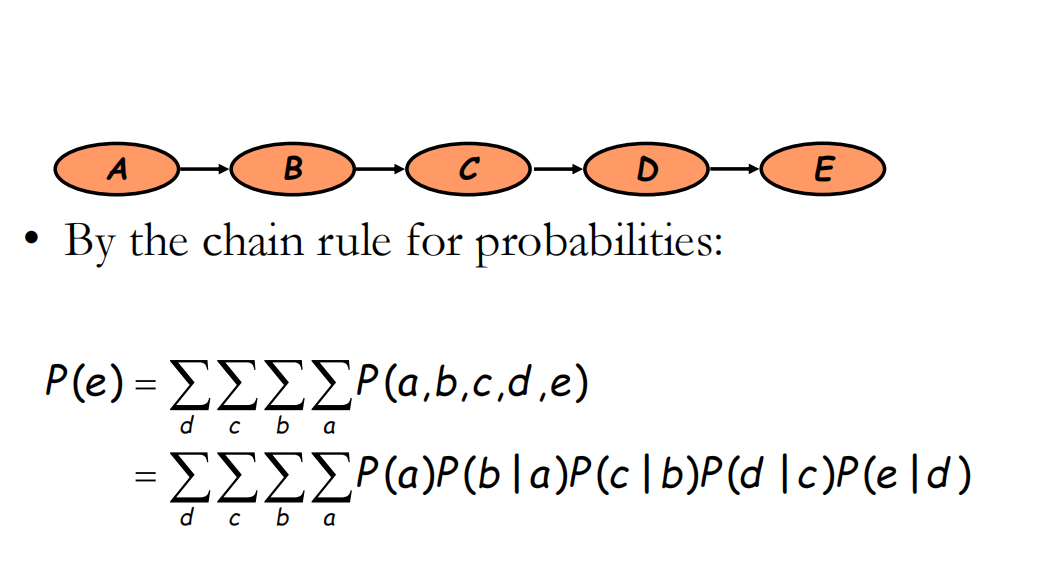可以通过从（Σa P(a)P(b|a))消除a，进而可以一步步的把a,b,c等消除掉
这就是direct variable elimination

2 消元法在隐马模型和马尔可夫随机场

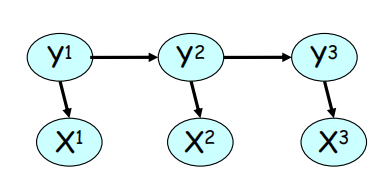初始条件：
\(\alpha_1(i)=\pi_i e_{i,x_1}\) 其中的$\pi_i$是 y1 的初始值，e则是x1的初始值
那么其递推公式是：
\(\alpha_{t+1}(i)=[\sum_{j=1}^N \alpha_t(j)t_{j,i}] e_{i,x_{t+1}}\) 最终统合：
\(P(X|\theta)=\sum_{i=1}^N \alpha_T(i)\) 对于这些比较简单的例子模型，可以直接通过消元法实现，但是只有消元法是不够的，我们还希望找到更加高效的算法

3 更复杂的贝叶斯网络

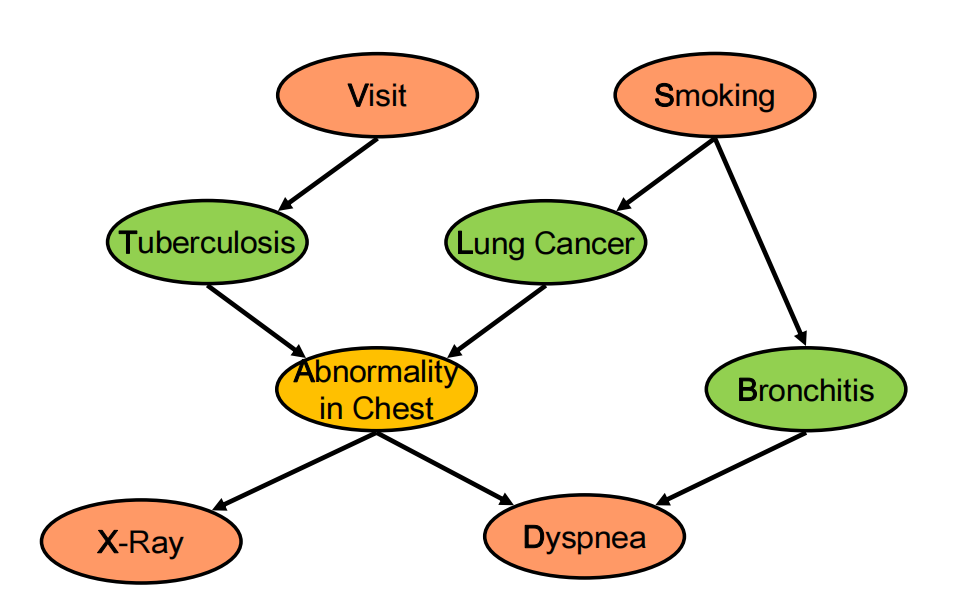根据这个图可以知道联合概率，但我们想知道P(D) (也就是P(Dyspnea))
首先因子分解：
\(P(V)P(S)P(T |V)P(L | S)P(B | S)P(A|T, L)P(X | A)P(D | A,B)\) 将条件概率的标记以factors简化书写：
\(\phi V (V) \phi S (S) \phi T (T,V)\phi L (L,S)\phi B (B,S)\phi A (A,T.L)\phi X (X, A)\phi D (D, A,B)\) 为了求P(D),需要eliminate: V,S,X,T,L,A,B
根据上述的因子分解定理：
先eliminate: V：
\(\tau_1(T)=\sum_V \phi_V(V)\phi_T(T,V)\) 此处的$\tau_1(T)=P(T)$ ，那么上述的因子分解可以改写为：
\(\tau_1(T) \phi S (S) \phi L (L,S)\phi B (B,S)\phi A (A,T.L)\phi X (X, A)\phi D (D, A,B)\) 那么重复上述过程，现状消除S:
\(\tau_2(L,B)=\sum_V\phi_S(S)\phi_L(L,S)\phi_B(B,S)\) 那么因子分解定理可以简写成：
\(\tau_1(T) \tau_2(L,B) \phi A (A,T.L)\phi X (X, A)\phi D (D, A,B)\) 接下来消除X:
\(\tau_3(A)=\sum_X \phi_X(X,A)\) 需要注意此处的$\tau_3(A)=1$
那么因子分解定理可以写出：

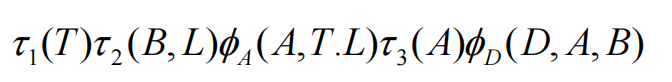
最后在消除T:

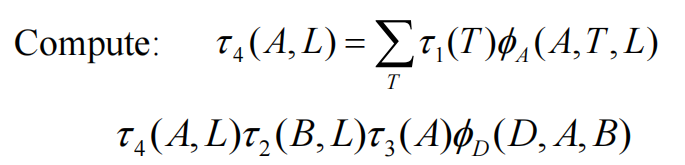
然后再消除L:

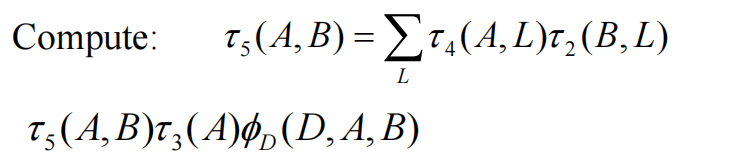
然后再消除A
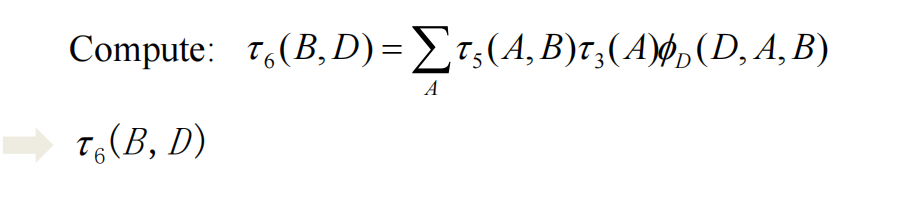最后只需要消除B:
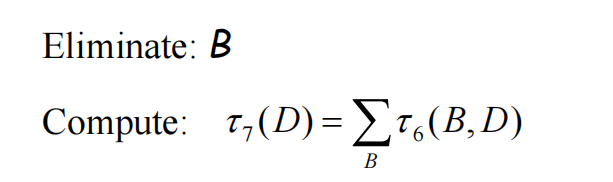\(P(D)=\tau_7(D)\)

对于有向图，一般是处理V结构后转化成无向图，然后再依次消元
为了减少计算成本，还可以把大的图的clique算好，以后只需要直接利用clique结果实现推断
有向图–>处理掉v structure（这里的HGJ也是v-structure,记得三角化——连上GJ） –> 处理掉四边形得到induced graph –> 再把其转换可以得到clique tree
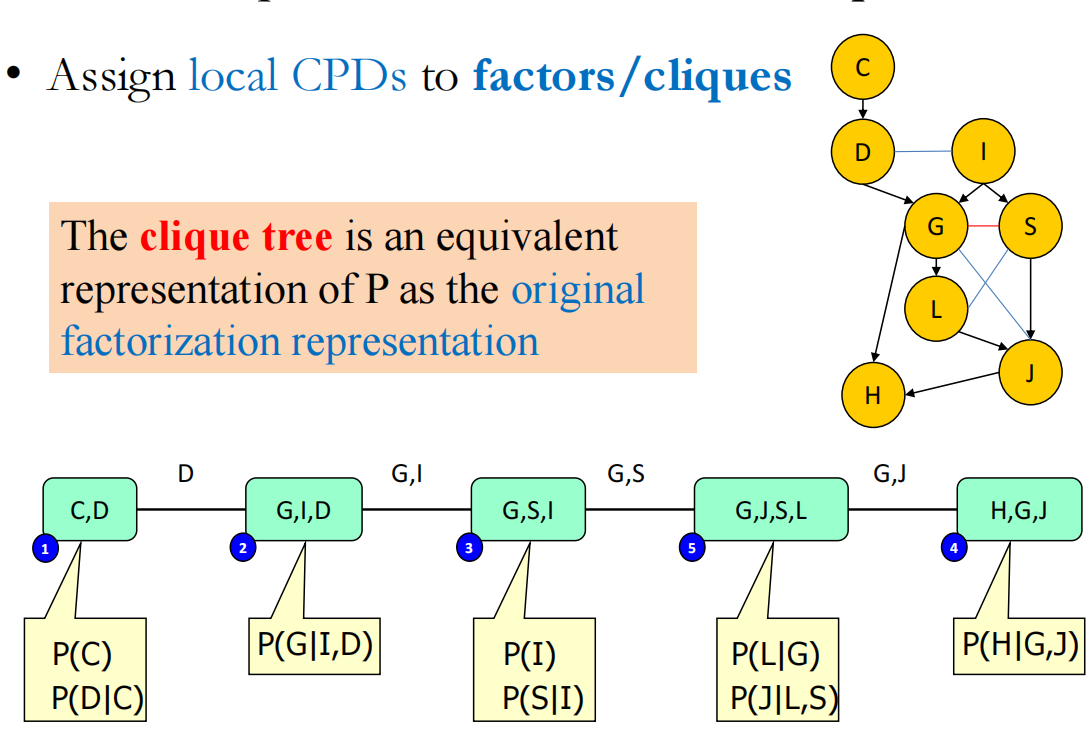需要注意的是，这里的clique tree 是选择最高阶的clique
每一个factors 的φi都是定义在clique上的
两边信息发到目标clique

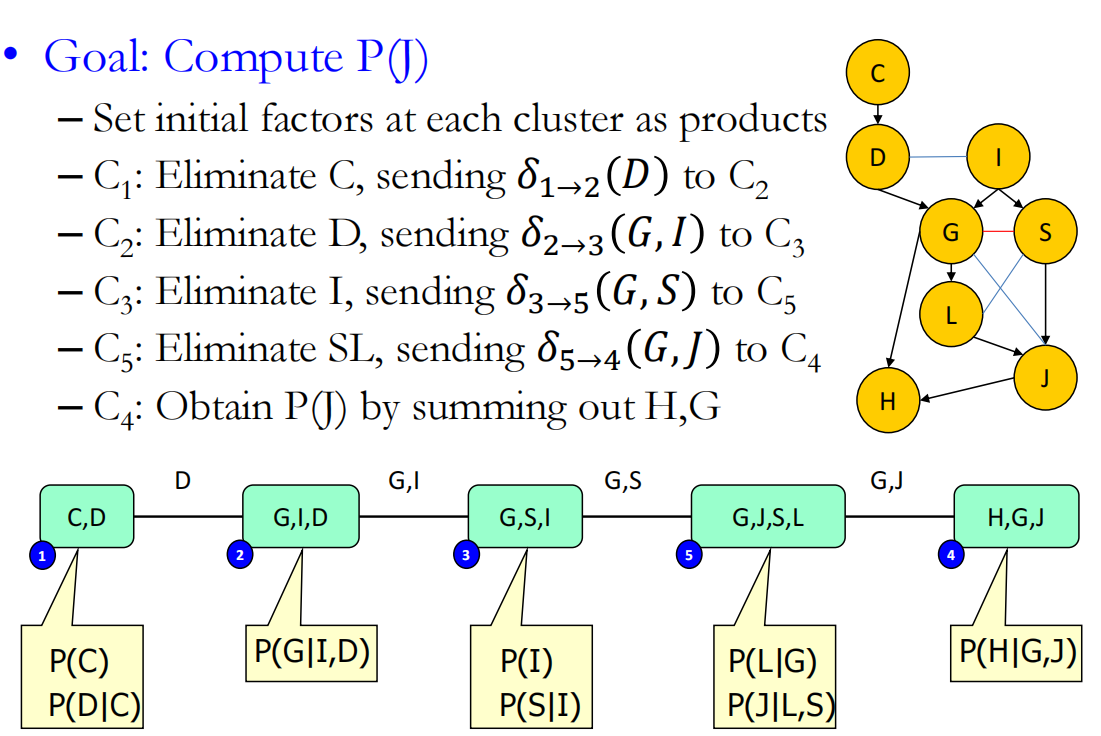
目标我们称之为根节点
例如对于如下的clique tree

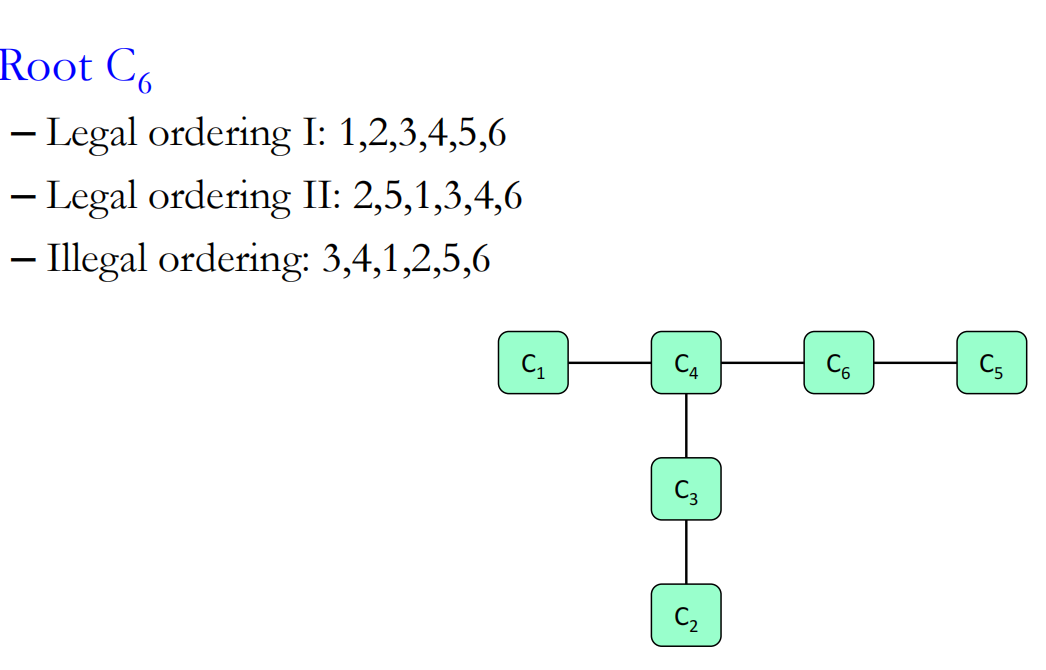
根节点是C6
第一个途径，首先1发信息到4，2发信息到3，3发信息到4，此时4都已经有1和3的节点了就可以4发到根节点6了，然后是5发信息到6
与之相反的就是第三个顺序，3发到4后直接4发信息到6就不合理，因为此时1还没发信息
clique tree就是为了简化使得让inference的消元法更加容易理解
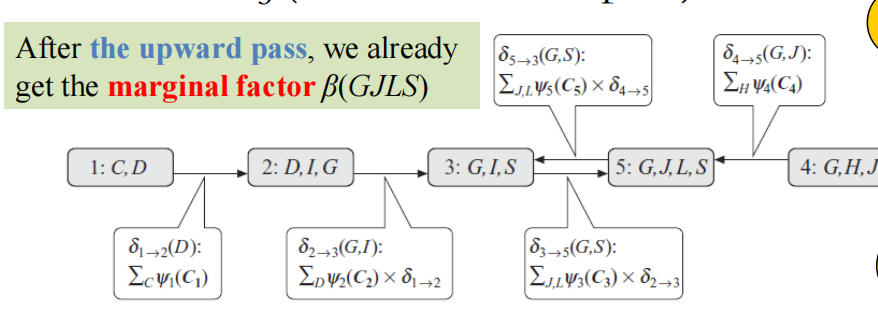现状已经把5节点的边缘概率算完了，只需要把其信息又发出去，那么就可以得到其他节点的边缘概率了
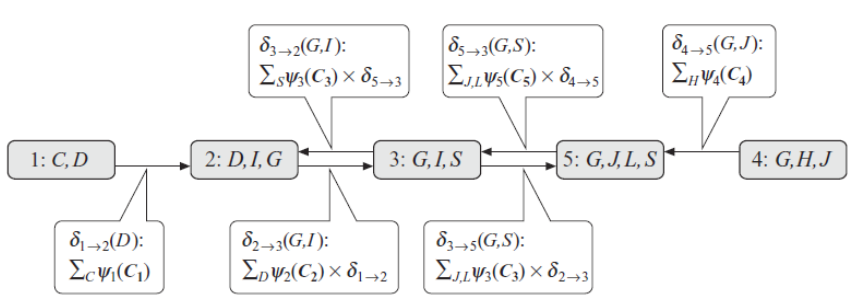（这一步称为downward pass）
经过了upward和downward两个步骤之后，整个网络都已经被校准了（每个节点都是其边缘概率)，整个模型就成为了稳态，这样变很方便进行query————这就是clique tree的calibration
**选择哪个作为根节点对于其结果没有影响 **

由于每条边上的信息被收录到旁边俩节点的边缘概率里，所以算总p的时候重复算了边上的信息，需要除去：
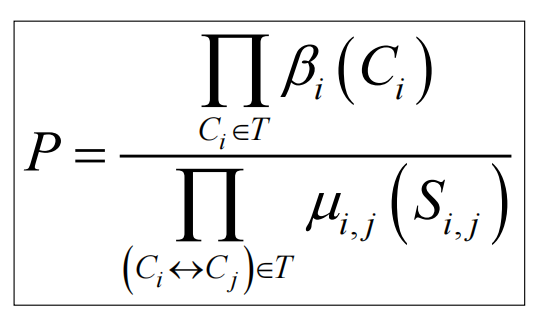例如：
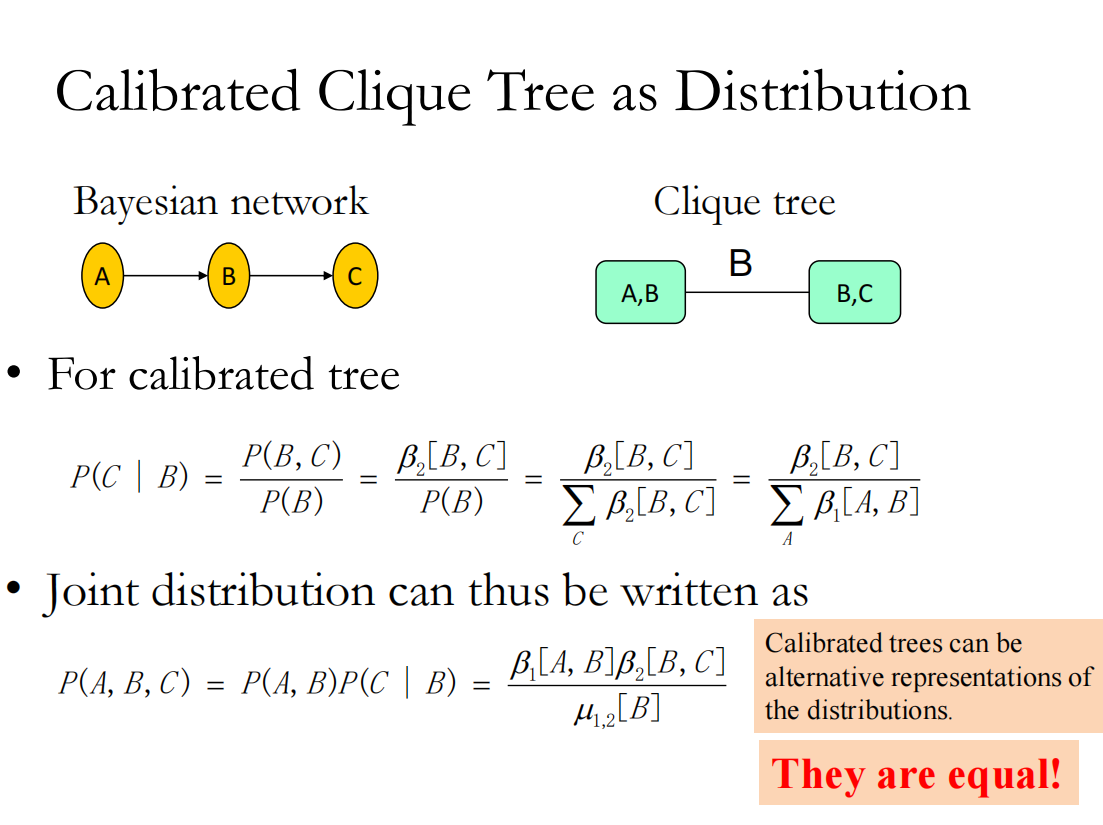还有不再固定根节点的信息传播，而是随便选择就开始发信息，需要保证的就是迭代很多轮之后整个clique tree能够达到稳态

clique tree就是原先概率图模型的等价表示，他的优势在于可以更好的帮助我们实现算法的设计

4 clique tree设计

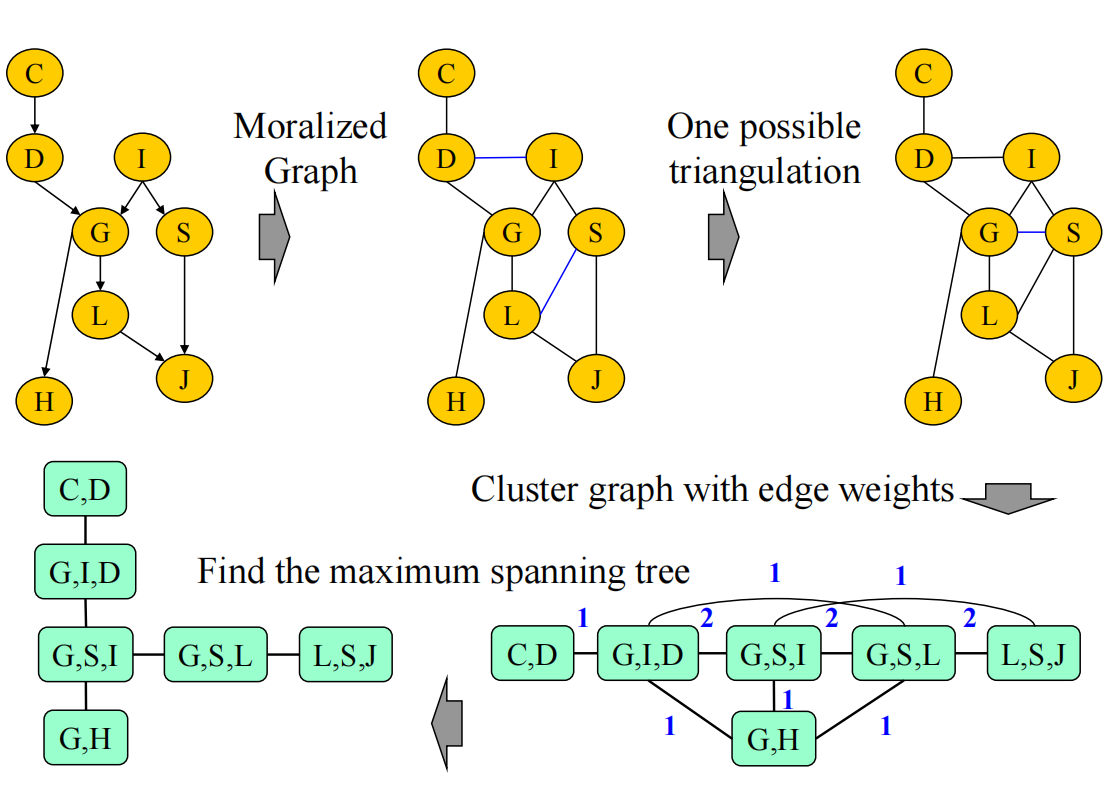
一定要先处理v-structure再处理多边形

5 loopy cluster graph

无向图如果不做三角化就会出现环状的情况：
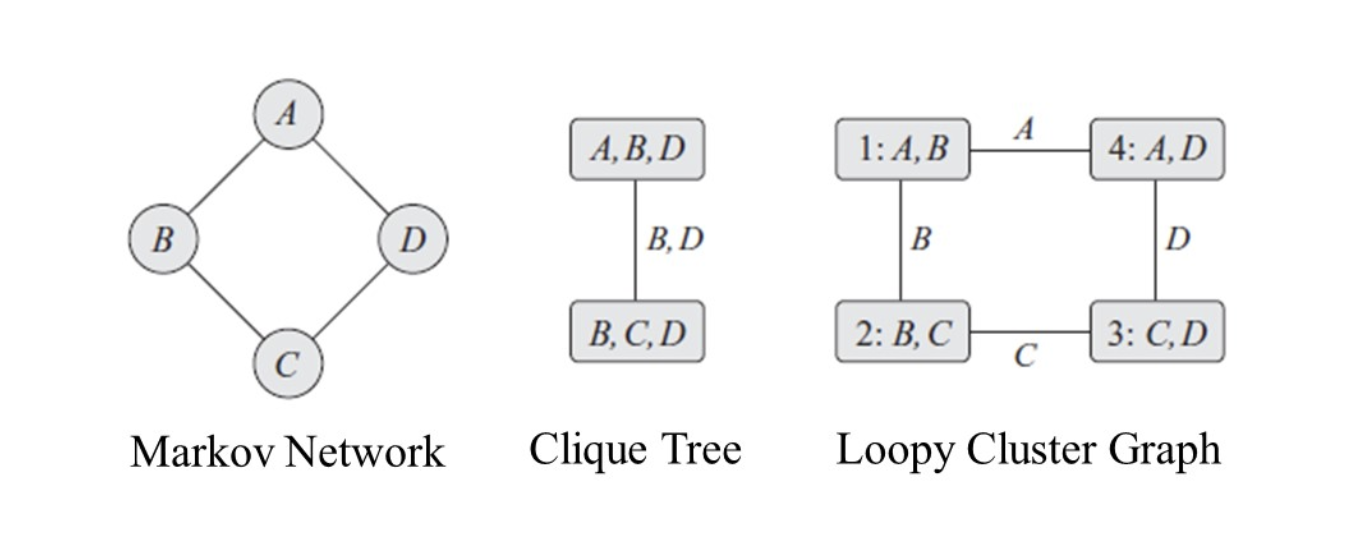这会使得A转一圈信息又回到了1
这一cluster graph没有理论基础，只是一个处理的算法，能算就完事
只需要满足Running Intersection Property即可
但这里是不能保证结果收敛，也不能保证收敛结果就是正确的边缘概率（在这里的belief propagation)