概率图模型6 概率图模型表示部分小结与进阶

2024-10-21

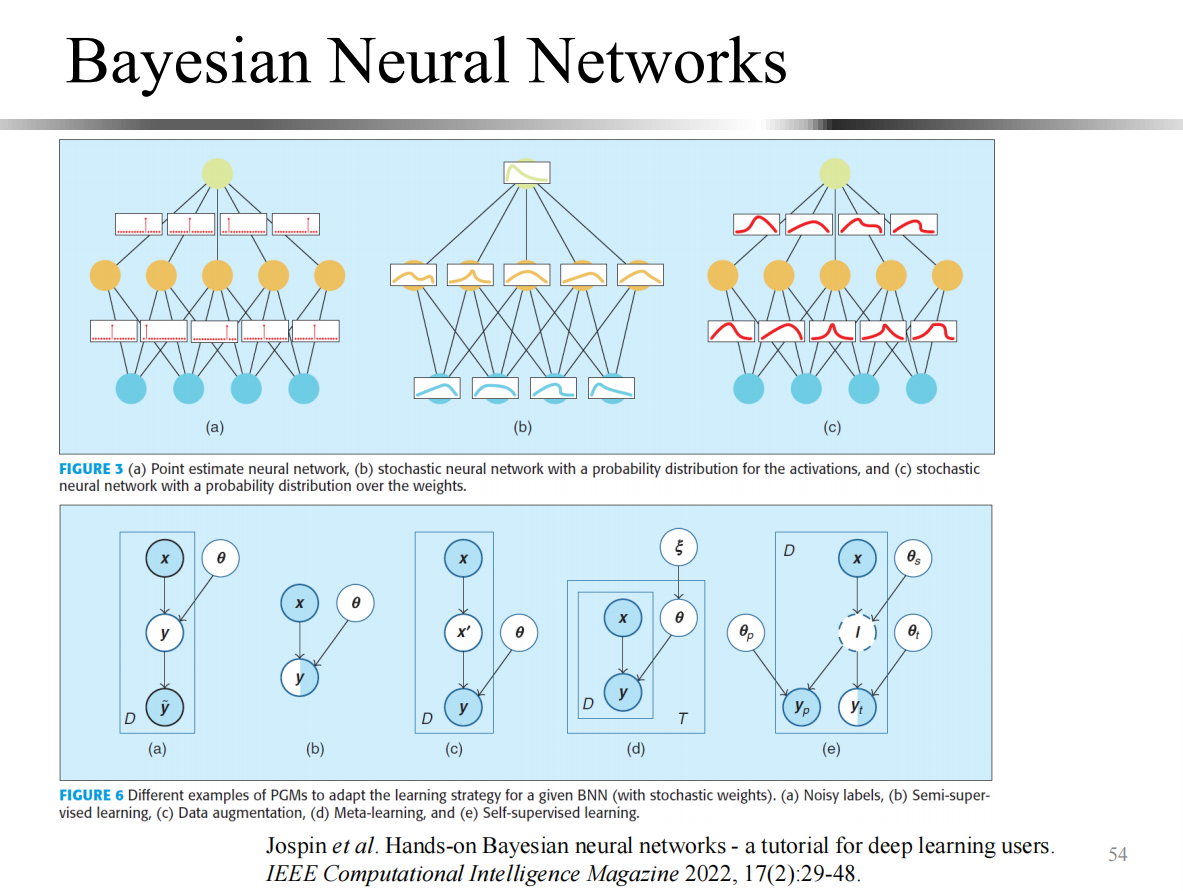
该笔记主要回顾了前一段时间所学习的概率图模型表示部分，同时介绍了一些更加前沿的研究

1 review

image-20241021100617654 动态序列模型就是把有向图用于研究序列的问题
表示部分的举例：
贝叶斯网络：

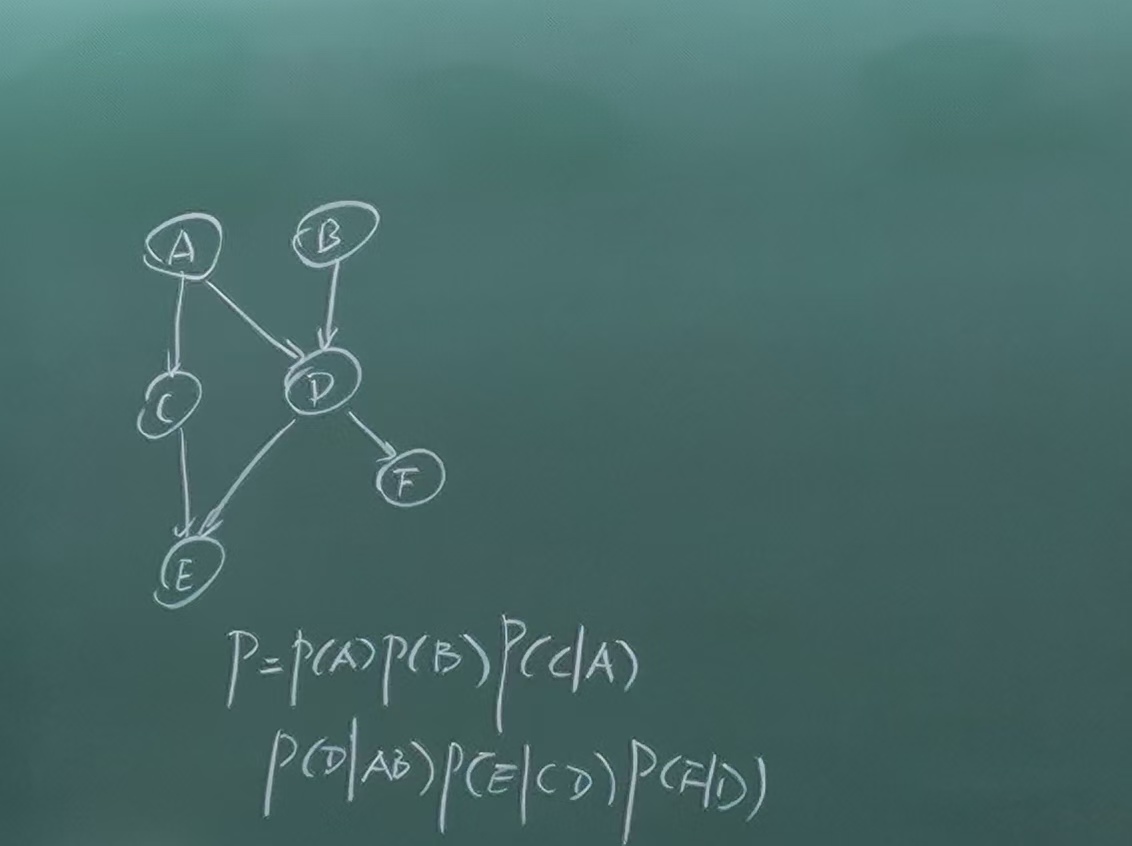506008128fa27a903e052f0ad773012 序列模型：

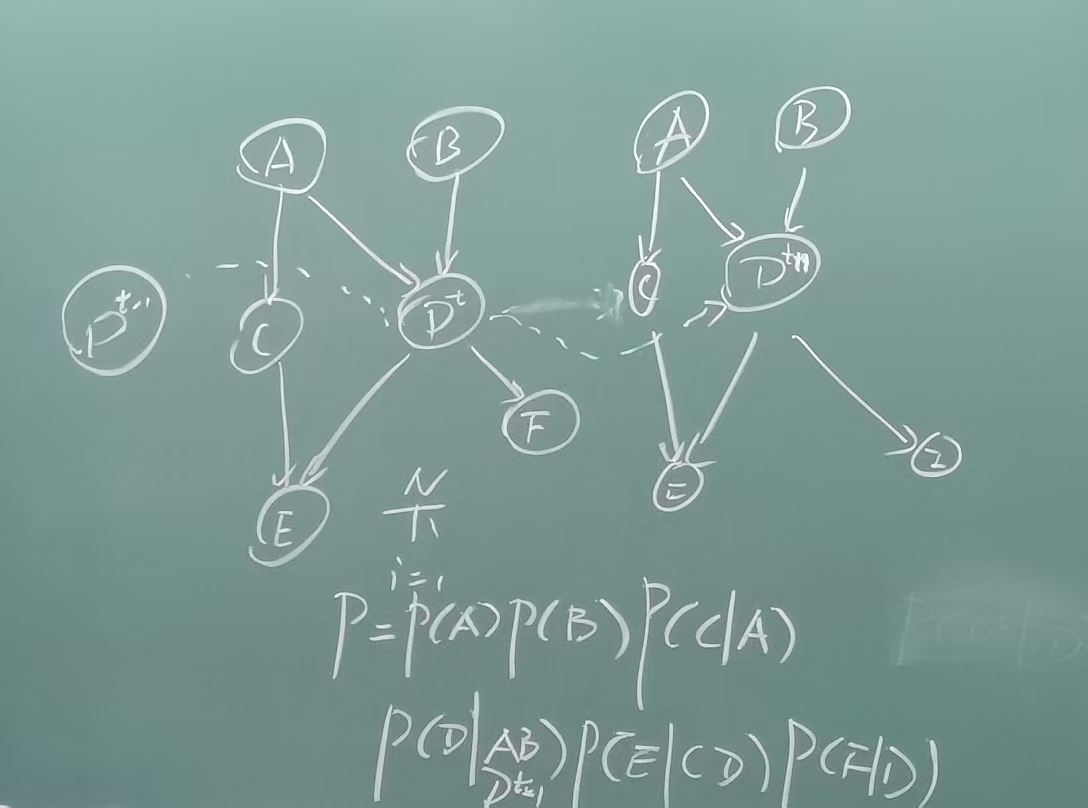d9ff7ce17969f8841642c265b699fab 马尔可夫毯：父节点，子节点，子节点的父节点
对于从有向图到无向图的转化：I(H)⊂I(G),需要做的是把V structure的父节点连起来，例如对于上述的贝叶斯网络，转换后即变为：

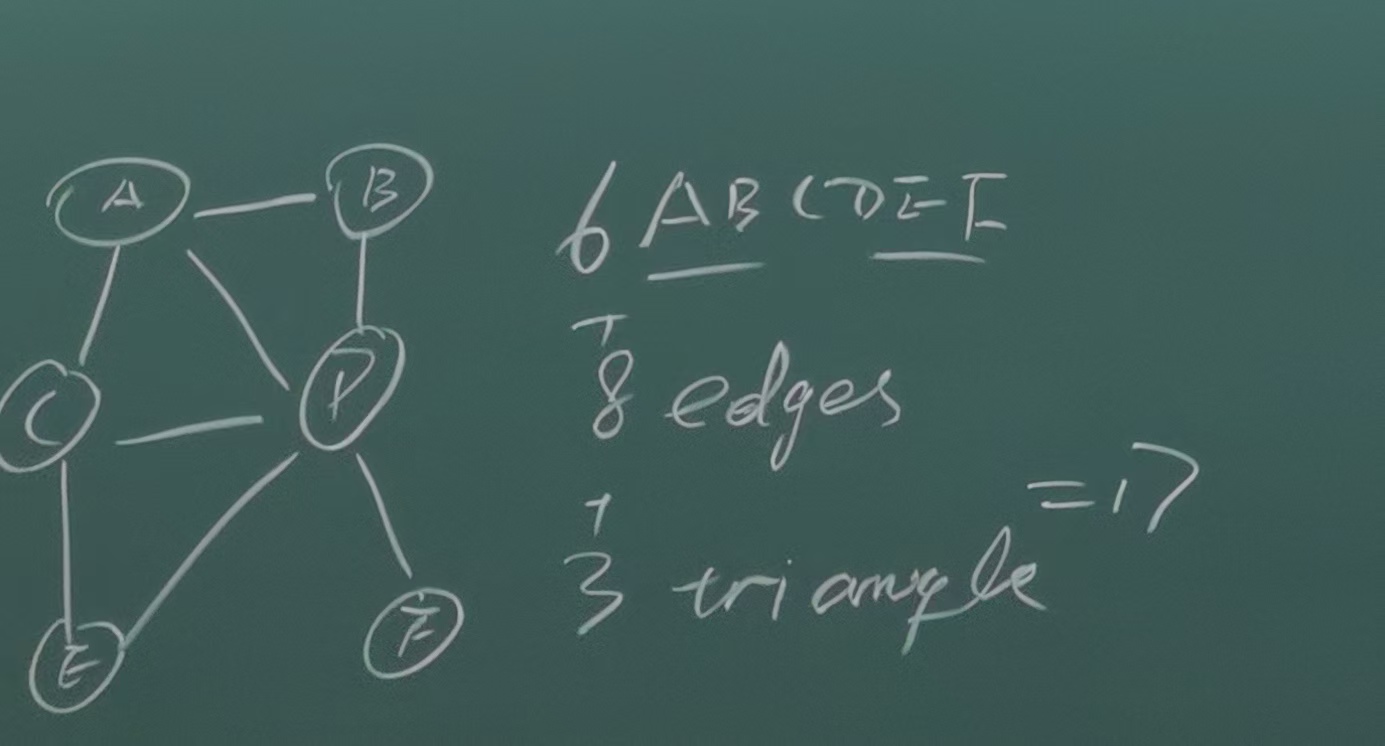
db514cfb539a8429bc4e23ab3f1be9d

对于有向图，分解完之后还需要对每个local CPD的内容进行设计

2 question solved way

image-20241021103042384

其中，设计隐变量是很重要的（且ai模型都无法帮助的）

image-20241021104124100 z用于降维，C用于混合模型，最终得到x：
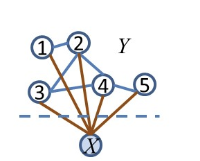
上述的三维分布每一组数据分布在一个平面里，上述S三维分布中有5个平面：

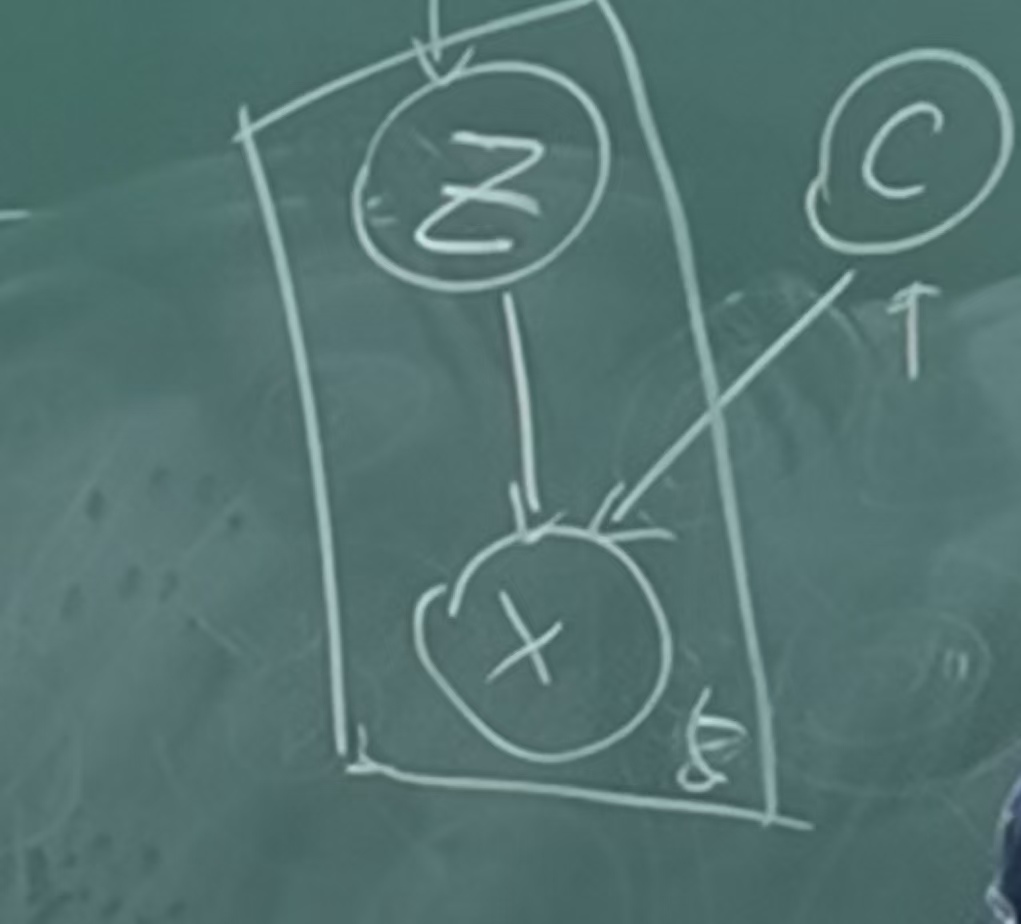
e925ce4670f0f6bf1bc314766b925a8

每次选择一个class label再选择一个z坐标，最后生成了数据x

3 Medel Conditional Information

image-20241021105644311 两类问题：生成模型/判别问题
model联合概率往往是生成模型，难度远高于model条件概率的判别模型
从HMM的生成模型到判别的MEMM(Max Entropy Markov Models):
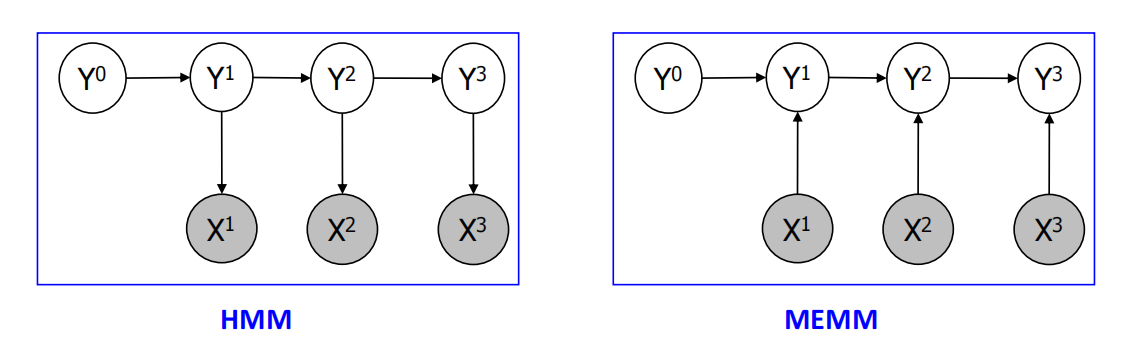
image-20241021105900784

conditional nodes:多了一个超脱于所有的节点的条件节点，相当于在条件的每一项后面都多一个x就行了
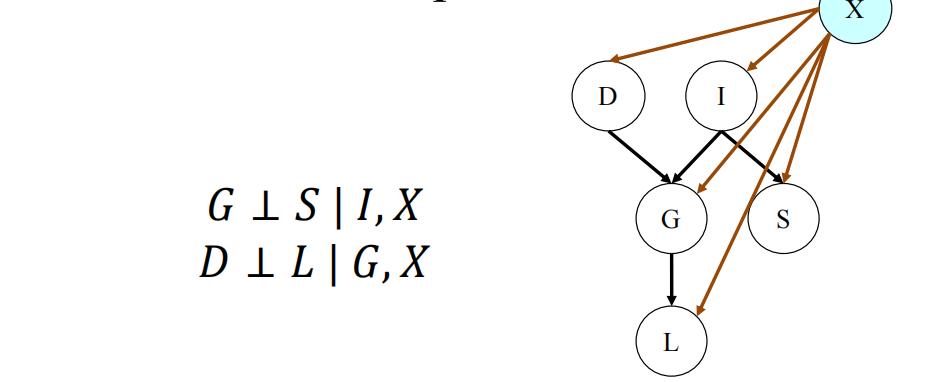image-20241021110056582 X是永远观测到的时候，对原图的节点的独立性是没有任何影响的
image-20241021110708212

此时，只含X的项就不需要包含，但其他所有和x相关的y的clique都需要保留（全都写出来最后把只含x的去掉即可）

建模的时候有时候会忽略高阶效应（这时仅剩下边和节点的影响项）——具体是否忽略高阶效应取决于实际的应用

判别模型的缺点是不能产生新的数据，且受分类边界上的影响较大（位于边界附近的异常值将导致误导性的判别平面）
判别模型需要的是有label的数据

4 Deep Structures

当初的现状：“Big” unlabeled data and “small” labeled data
如何建模好大量的非标记数据（抽取特征，传统的使用的是PCA,Hinton & Salakhutdinov. Reducing the dimensionality of data with neural networks. Science 2006 做了一个pretraining的限制性玻尔兹曼积RBM进行降维
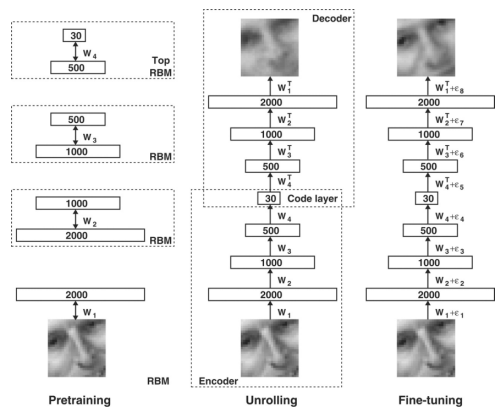image-20241021114106199 通过端到端的loss function来学习
Web resources:

  • Machine intelligence (Nature 521:7553, 435)

image-20241021120843494