该笔记主要介绍概率图模型有向图中的隐马尔可夫模型HMM
1 review
Factorization Theorem
- variable
- design the network
- design local CPD
markov/Memoryless Property
对于角标赋予序列的含义之后，马尔可夫链就有时间上的分布意义了——时间上是稳态的
eg. random walk
eg2. 人机交互，Y是视频资料；Z是声音信息
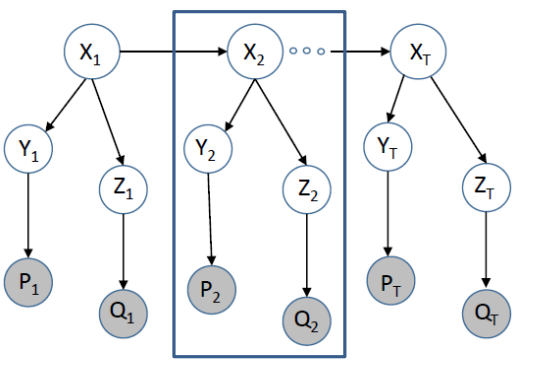建模多一层以便描述噪声的问题——概率图形中经常引入一些在现实中很难检测的变量（比如噪声等)
这也是本节主要想了解和解释的部分，上述结构假设是时不变系统
一般就有两类参数，一个是内部时间窗的参数，一个是时间窗口之间的参数
2 Hidden Markov Models
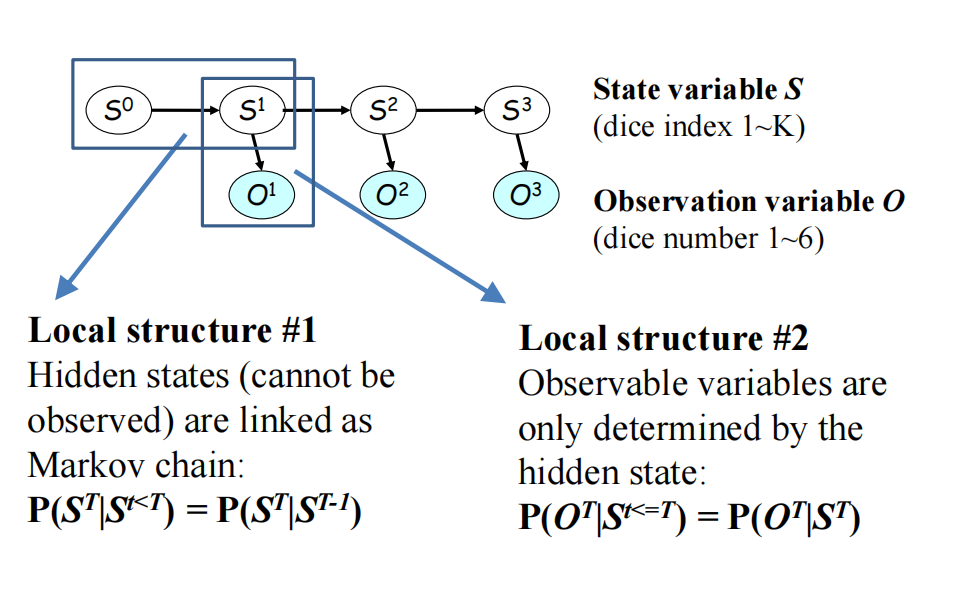其实这里的s就是隐变量，因为我们没有S的数据
满足各态便利性时就可以最后收敛成时间平稳的稳态
保证个态遍历可以给有些0的地方加一些特别小的数
其他应用：基因组上的序列（不一定要求是时间轴上的序列)
2.1 Calculations in HMMs
-
Problem 1:$ 𝑃(𝑿 𝜽)$ , given the model and the
observation sequence, infer the probability of
getting that observation sequence from the model
-
Problem 2: $argmax_𝑌 𝑷(𝑿, 𝒀 𝜽)$, given the model and the observation sequence, infer the hidden labels of the sequence -
Problem 3: $argmax_𝜃 𝑷(𝑿 𝜽)$, if parameters are unknown, learn them from the observation sequence
2.2 𝑃 (𝑿|𝜽）的计算
如果没有引入隐变量描述马尔可夫模型的话，所有观测变量将不独立的全连接，引入隐变量后就会增加独立性进而简化模型参数数量
因子分解将父节点参数塞回
前向/后向算法：
$\pi_i$是启动参数,e则是观测的参数
\(\alpha_1(i)=P(Y_1=i)P(x_1|Y_1=i)\)
实际上$[\sum_{j=1}^N \alpha_t(j)t_{j,i}]$就是$P(Y_{t=i}|Y_{t-1})$
倒退过程则如下：
但实际上正向和倒推最后得到的结果是一样的
2.3 argmax_Y 𝑷(𝑿, 𝒀|𝜽)的计算——算哪个Y使得这个最大概率值可以取到
需要记录每一步的节点概率是怎么来的
2.4 argmax_𝜽 𝑷(𝑿|𝜽)的求解
需要求解：
\(argmax_\theta=\sum_YP(XY|\theta)\)
由于是隐变量，所以Y和θ往往是不知道的，一个解决的方法是通过迭代的方法
\(\theta^0-->Y^0-->\theta^1-->Y^1-->\cdots\)
但这一方法不保证每次都收敛，即便收敛也不能保证全局最优
\(\xi_t(i,j)=P(y_t=i,y_{t+1}=j|X,\theta)\)
再用上面的参数求解出t和e
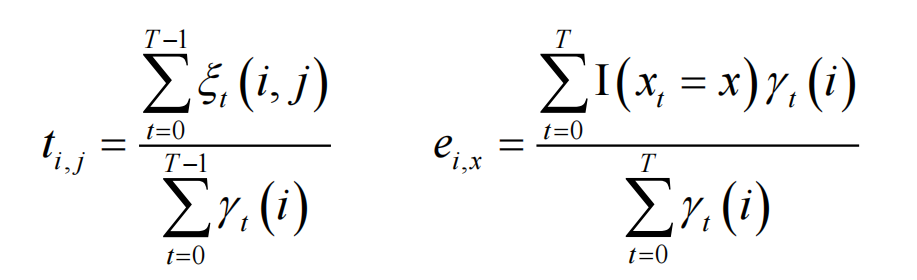
只需要不断重复迭代即可：
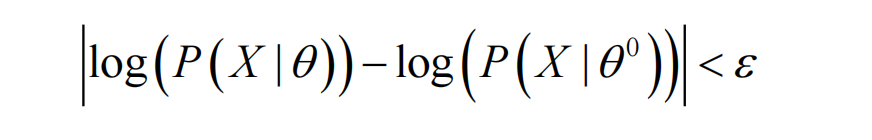
口诀：父节点，子节点，子节点的父节点
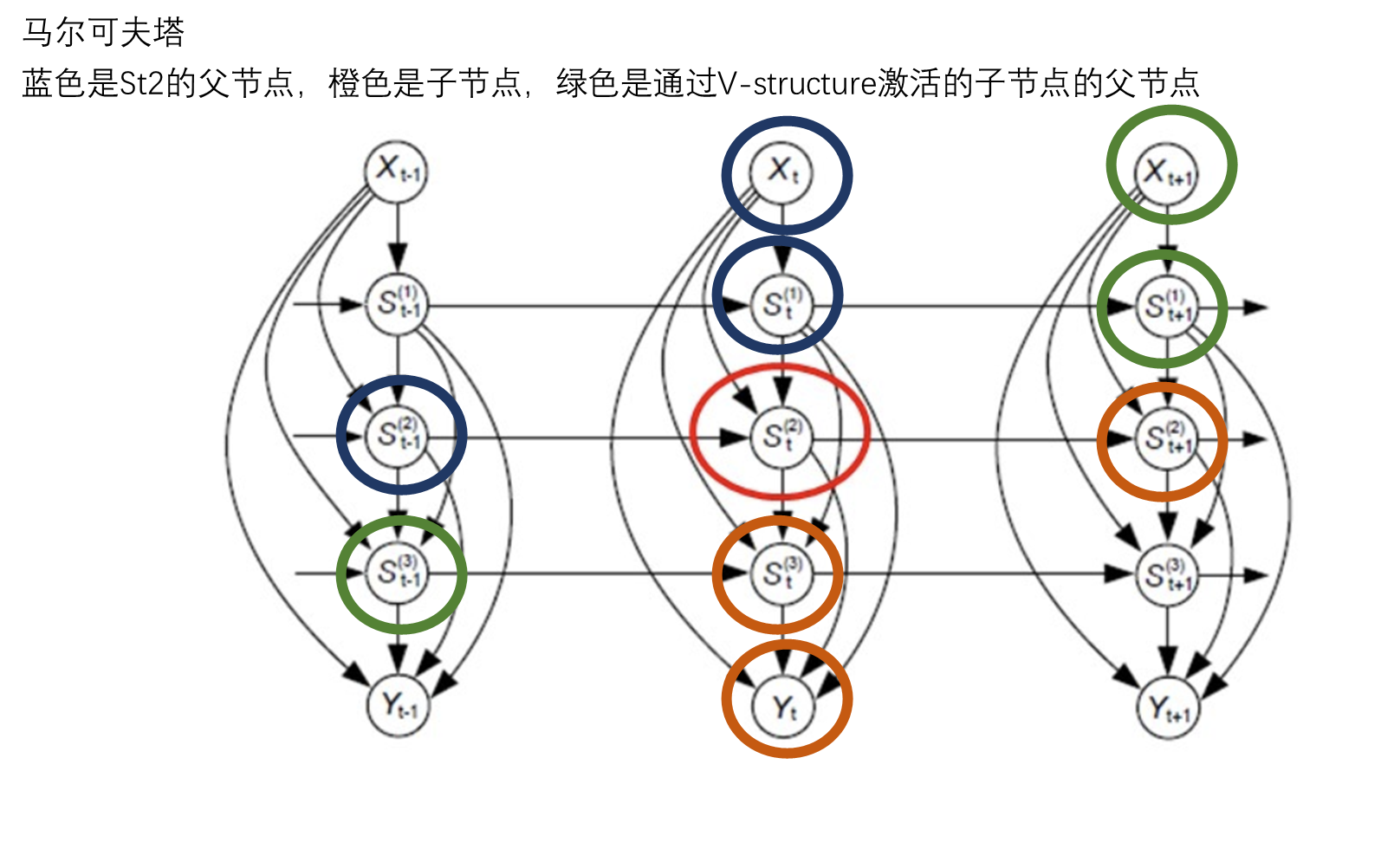
实际上RNN就是参照马尔可夫链来构建的，LSTM相较于RNN而言由于更有长程相关而变得更有用（RNN的马尔可夫性太强）